基本介紹
- 中文名:古希臘三大幾何問題
- 外文名:Three impossible ruler-and-compass constructions from ancient Greek mathematicians
- 學科:平面幾何
- 內容:立方倍積、化圓為方、三等分角
問題引入
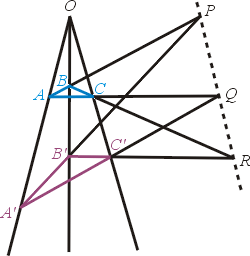
具體內容
立方倍積

化圓為方
三等分角
結果意義
 德國數學家林德曼
德國數學家林德曼
三大幾何問題一般指本詞條


 德國數學家林德曼
德國數學家林德曼
古希臘三大幾何問題既引人入勝,又十分困難。問題的妙處在於它們看非常簡單,而實際上卻有著深刻的內涵。它們都要求作圖只能使用圓規和無刻度的直尺,而且只能有限次地...
幾何三大問題(Three major geometric problems)是指二千四百多年前,古希臘幾何學家提出的尺規作圖問題(ruler-and-compass construction),即只使用圓規和直尺,並且只...
平面幾何三大難題編輯 鎖定 尺規作圖的限定 平面幾何作圖限制只能用直尺、圓規,而這裡所謂的直尺是指沒有刻度只能畫直線的尺。 用直尺與圓規當然可以做出許多種之...
古希臘幾何作圖的三大問題是:①化圓為方,求作一正方形,使其面積等於一已知圓;②三等分任意角;③倍立方,求作一立方體,使其體積是一已知立方體的兩倍。這些問題...
化圓為方問題(problem of quadrature of circle)是二千四百多年前古希臘人提出的三大幾何作圖問題之一,即求作一個正方形,使其面積等於已知圓的面積。...
立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等,是幾何三大問題之一。假設已知立方體的棱長...
《初等幾何的著名問題》是高等教育出版社2005年7月1日出版的圖書,作者是(德國)克萊因。該書是數學家F.Klein1894年在德國哥廷根的一個講稿,主要討論了初等幾何的...
三等分角是古希臘三大幾何問題之一。三等分角是古希臘幾何尺規作圖當中的名題,和化圓為方、倍立方問題被並列為古代數學的三大難題之一,而如今數學上已證實了...
《著名幾何問題及其解法》是2008年高等教育出版社出版的圖書,作者是(美)B.波爾德。本書通過穿插歷史資料和生動的故事來講解了幾個著名幾何問題及其解法。...
尺規作圖不能問題就是不可能用尺規作圖完成的作圖問題。這其中最著名的是被稱為幾何三大問題的古典難題:三等分角問題:三等分一個任意角;倍立方問題:作一個立方體...
數學難題可以是指那些歷經長時間而仍未有解答/完全解答的數學問題。古今以來,一些特意提出的數學難題有:平面幾何三大難題、希爾伯特的23個問題、世界三大數學猜想、...
幾何,就是研究空間結構及性質的一門學科。它是數學中最基本的研究內容之一,與...4 幾何作圖 ▪ 尺規作圖 ▪ 三大問題 5 幾何原本 6 幾何基礎 ▪...
倍立方問題和三等分角問題、化圓為方問題共稱為尺規作圖不能問題,也叫做古希臘三大幾何問題。它指的是:作一個立方體,使它的體積是已知立方體的體積的兩倍。...
同義詞 世界近代三大數學難題一般指世界三大數學猜想 世界三大數學猜想即費馬猜想、...猜想時,使用了沙伐爾維奇猜想、雅可比簇、高、同源和台特猜想等大量代數幾何知識...
《數學上的未解難題》是2010年7月1日中國出版集團、世界圖書出版公司出版的圖書...漫談尺規作圖三大難題幾何奧妙探索形的起源幾何圖形實驗幾何《幾何原本》...
