基本介紹
基本介紹


 圖1.倍立方問題
圖1.倍立方問題背景介紹
相關傳說
尺規作圖法
- 直尺:一側為無窮長的直線,沒有刻度也無法標識刻度的工具。只可以讓筆摹下這個直線的全部或一部分。
- 圓規:由兩端點構成的工具。可以在保持兩個端點之間的距離不變的情況下,將兩個端點同時移動,或者只固定其中一個端點,讓另一個端點移動,作出圓弧或圓。兩個端點之間的距離只能取已經作出的兩點之間的距離,或者任意一個未知的距離。
問題敘述

倍平方問題



方法













 圖2.用有刻度的直尺來進行倍立方
圖2.用有刻度的直尺來進行倍立方證明

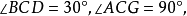




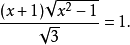




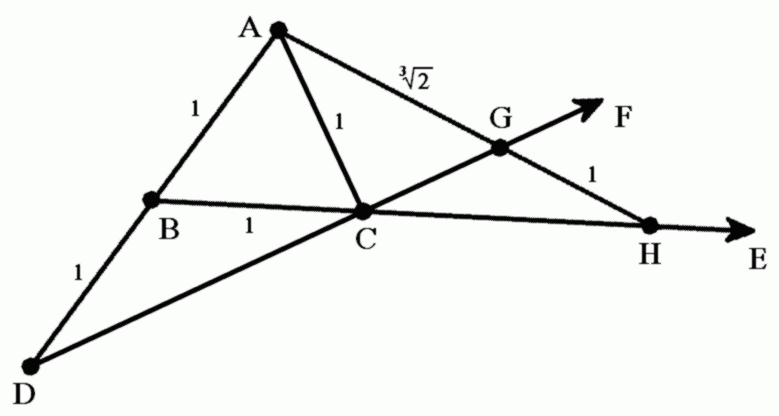
立方倍積一般指本詞條


 圖1.倍立方問題
圖1.倍立方問題
















 圖2.用有刻度的直尺來進行倍立方
圖2.用有刻度的直尺來進行倍立方
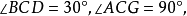




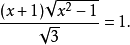




立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等,是幾何三大問題之一。假設已知立方體的棱長...
化圓為方,立方倍積和三等分角這三大古希臘幾何作圖難題的結果又是如何被證明的呢?帶著問題讓我們來探究一下。(1)化圓為方問題的結果...
尺規作圖不能問題就是不可能用尺規作圖完成的作圖問題。這其中最著名的是被稱為幾何三大問題的古典難題:三等分角問題:三等分一個任意角;倍立方問題:作一個立方體...
立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等,是幾何三大問題之一。假設已知立方體的棱長...
由於對尺規作圖的限制,使得一些貌似簡單的幾何作圖問題無法解決.最著名的是被稱為幾何三大問題的三個古希臘古典作圖難題:立方倍積問題、三等分任意角問題和化圓為...
希氏曾致力於“化圓為方”和“立方倍積”問題的研究,月形定理是其之出發點,由於他的疏忽,曾使人們一度認為化圓為方十分容易,不少人上了當。他把月形定理...
由於對尺規作圖的限制,使得一些貌似簡單的幾何作圖問題無法解決.最著名的是被稱為幾何三大問題的三個古希臘古典作圖難題:立方倍積問題、三等分任意角問題和化圓為...
18.2立方倍積、三等分任意角與化圓為方 第十九章正n邊形的尺規作圖 19.1把正n邊形的可作性歸結為一些簡單的情況 19.2有關□邊形的兩個域列 19.3分圓...
立方倍積、三等分角、化圓為方、正多邊形作圖、方程的根式解和費馬大定理,這些是最著名的數學歷史性難題,影響深遠。[1] 古希臘名題與現代數學圖書目錄 編輯 ...
