基本介紹
費馬大定理,四色定理,哥德巴赫猜想,
費馬大定理
內容
當整數n > 2時,關於x,y,z的不定方程 x^n + y^n = z^n 無正整數解。
簡介
這個定理,本來又稱費馬最後的定理,由17世紀法國數學家費馬提出,而當時人們稱之為“定理”,並不是真的相信費馬已經證明了它。雖然費馬宣稱他已找到一個絕妙證明,德國佛爾夫斯克宣布以10萬馬克作為獎金獎給在他逝世後一百年內,第一個證明該定理的人,吸引了不少人嘗試並遞交他們的“證明”。在一戰之後,馬克大幅貶值,該定理的魅力也大大地下降。 懷爾斯和費馬大定理
懷爾斯和費馬大定理
 懷爾斯和費馬大定理
懷爾斯和費馬大定理但經過三個半世紀的努力,這個世紀數論難題才由普林斯頓大學英國數學家安德魯·懷爾斯和他的學生理查·泰勒於1994年成功證明。證明利用了很多新的數學,包括代數幾何中的橢圓曲線和模形式,以及伽羅華理論和Hecke代數等,令人懷疑費馬是否真的找到了正確證明。而安德魯·懷爾斯(Andrew Wiles)由於成功證明此定理,獲得了1998年的菲爾茲獎特別獎以及2005年度邵逸夫獎的數學獎。
發現
費馬在閱讀丟番圖《算術》拉丁文譯本時,曾在第11卷第8命題旁寫道:“將一個立方數分成兩個立方數之和,或一個四次冪分成兩個四次冪之和,或者一般地將一個高於二次的冪分成兩個同次冪之和,這是不可能的。關於此,我確信已發現了一種美妙的證法 ,可惜這裡空白的地方太小,寫不下。”(拉丁文原文: "Cuius rei demonstrationem mirabilem sane detexi。 Hanc marginis exiguitas non caperet。")
畢竟費馬沒有寫下證明,而他的其它猜想對數學貢獻良多,由此激發了許多數學家對這一猜想的興趣。數學家們的有關工作豐富了數論的內容,推動了數論的發展。對很多不同的n,費馬定理早被證明了。但數學家對一般情況在首二百年內仍對費馬大定理一籌莫展。
莫德爾猜想
1983年,聯邦德國數學家伐爾廷斯證明了莫德爾猜想,從而翻開了費馬大定理研究的新篇章,伐爾廷斯獲得1982年菲爾茲獎。
伐爾廷斯於1954年7月28日生於聯邦德國的傑爾森柯琛,並在那裡渡過了學生時代,而後就學於內斯濤德教授門下學習數學。1978年獲得博士學位。他作過研究員、助教,現在是波恩大學的教授。他在數學上的興趣開始於交換代數,以後轉向代數幾何。
1922年,英國數學家莫德爾提出一個著名猜想,人們叫做莫德爾猜想。按其最初形式,這個猜想是說,任一不可約、有理係數的二元多項式,當它的“虧格”大於或等於2時,最多只有有限個解。記這個多項式為f(x,y),猜想便表示:最多存在有限對數偶xi,yi∈Q,使得f(xi,yi)=0。
後來,人們把猜想擴充到定義在任意數域上的多項式,並且隨著抽象代數幾何的出現,又重新用代數曲線來敘述這個猜想了。因此,伐爾廷斯實際上證明的是:任意定義在數域K上,虧格大於或等於2的代數曲線最多只有有限個K一點。
數學家對這個猜想給出各種評論,總的看來是消極的。 1979年利奔波姆說:“可以有充分理由認為,莫德爾猜想的獲證似乎還是遙遠的事。”
對於“猜想”,1980年威爾批評說:“數學家常常自言自語道:要是某某東西成立的話,‘這就太棒了’(或者‘這就太順利了’)。有時不用費多少事就能夠證實他的推測,有時則很快否定了它。但是,如果經過一段時間的努力還是不能證實他的預測,那么他就要說到‘猜想’這個詞,既便這個東西對他來說毫無重要性可言。絕大多數情形都是沒有經過深思熟慮的。”因此,對莫德爾猜想,他指出:我們稍許來看一下“莫德爾猜想”。它所涉及的是一個算術家幾乎不會不提出的問題;因而人們得不到對這個問題應該去押對還是押錯的任何嚴肅的啟示。
然而,時隔不久,1983年伐爾廷斯證明了莫德爾猜想,人們對它有了全新的看法。在伐爾廷斯的文章里,還同時解決了另外兩個重要猜想,即台特和沙伐爾維奇猜想,它們同莫德爾猜想具有同等重大意義。
這裡主要解釋一下莫德爾猜想,至於證明就不多講了。 所謂代數曲線,粗略一點說,就是在包含K的任意域中,f(x,y)=0的全部解的集合。
令F(x,y,z)為d次齊次多項式,其中d為f(x,y)的次數,並使F(x,y,1)=f(x,y),那么f(x,y)的虧格g為
g≥(d-1)(d-2)/2
當f(x,y)沒有奇點時取等號。
費馬多項式x^n+y^n-1沒有奇點,其虧格為(n-1)(n-2)/2。當n≥4時,費馬多項式滿足猜想的條件。因此,xn+yn=zn最多只有有限多個整數解。
為什麼猜想中除去了f(x,y)的虧格為0或1的情形,即除去了f(x,y)的次數d小於或等於3的情形呢?我們說明它的理由。
d=1時,f(x,y)=ax+by+c顯然有無窮多個解。
d=2時,f(x,y)可能沒有解,例如f(x,y)=x2+y2+1;但是如果它有一個解,那么必定有無窮多個解。我們從幾何上來論證這一點。設P是f(x,y)解集合中的一點,令l表示一條不經過點P的直線(見上圖)。對l上坐標在域K中的點Q,直線PQ通常總與解集合交於另一點R。當Q在l上取遍無窮多個K—點時,點R的集合就是f(x,y)的K—解的無窮集合。例如把這種方法用於x2+y2-1,給出了熟知的參數化解:
當F(X,Y,Z)為三次非奇異(即無奇點)曲線時,其解集合是一個所謂橢圓曲線。我們可用幾何方法做出一個解的無窮集。但是,對於次數大於或等於4的非奇異曲線F,這種幾何方法是不存在的。雖然如此,卻存在稱為阿貝爾簇的高維代數簇。研究這些阿貝爾簇構成了伐爾廷斯證明的核心。
伐爾廷斯在證明莫德爾猜想時,使用了沙伐爾維奇猜想、雅可比簇、高、同源和台特猜想等大量代數幾何知識。 莫德爾猜想有著廣泛的套用。比如,在伐爾廷斯以前,人們不知道,對於任意的非零整數a,方程y2=x5+a在Q中只有有限個
有限組互質
1983年,en:Gerd Faltings證明了Mordell猜測,從而得出當n > 2時(n為整數),只存在有限組互質的a,b,c使得a^n + b^n = c*n。
Gerhard Frey
1986年,Gerhard Frey 提出了“ ε-猜想”:若存在a,b,c使得a^n + b^n = c^n,即如果費馬大定理是錯的,則橢圓曲線y^2 = x(x - a^n)(x + b^n) 會是谷山-志村猜想的一個反例。Frey的猜想隨即被Kenneth Ribet證實。此猜想顯示了費馬大定理與橢圓曲線及模形式的密切關係。
懷爾斯和泰勒
1995年,懷爾斯和泰勒在一特例範圍內證明了谷山-志村猜想,Frey的橢圓曲線剛好在這一特例範圍內,從而證明了費馬大定理。
懷爾斯
懷爾斯證明費馬大定理的過程亦甚具戲劇性。他用了七年時間,在不為人知的情況下,得出了證明的大部分;然後於1993年6月在劍橋大學的一個討論班上宣布了他的證明,並瞬即成為世界頭條。不過在審批證明的過程中,專家發現了一個缺陷。懷爾斯和泰勒然後用了近一年時間改進了它,在1994年9月以一個之前懷爾斯拋棄過的方法得到成功,這部份的證明與岩澤理論有關。他們的證明刊在1995年的數學年刊(en:Annals of Mathematics)之上。
n=3
歐拉證明了n=3的情形,用的是唯一因子分解定理。
n=4
費馬自己證明了n=4的情形。
n=5
1825年,狄利克雷和勒讓德證明了n=5的情形,用的是歐拉所用方法的延伸,但避開了唯一因子分解定理。
n=7
1839年,法國數學家拉梅證明了n=7的情形,他的證明使用了跟7本身結合的很緊密的巧妙工具,只是難以推廣到n=11的情形;於是,他又在1847年提出了“分圓整數”法來證明,但沒有成功。
理想數
庫默爾在1844年提出了“理想數”概念,他證明了:對於所有小於100的素指數n,費馬大定理成立,此一研究告一階段。
n<1,000,000
至1991年對費馬大定理指數n<1,000,000費馬大定理已被證明,但對指數n>1,000,000沒有被證明。
谷山——志村猜想
1955年,日本數學家谷山豐首先猜測橢圓曲線於另一類數學家們了解更多的曲線——模曲線之間存在著某種聯繫;谷山的猜測後經韋依和志村五郎進一步精確化而形成了所謂“谷山——志村猜想”,這個猜想說明了:有理數域上的橢圓曲線都是模曲線。這個很抽象的猜想使一些學者搞不明白,但它又使“費馬大定理”的證明向前邁進了一步。
兩者關係
1985年,德國數學家弗雷指出了谷山——志村猜想”和費馬大定理之間的關係;他提出了一個命題 :假定“費馬大定理”不成立,即存在一組非零整數A,B,C,使得A的n次方+B的n次方=C的n次方(n>2),那么用這組數構造出的形如y的平方=x(x+A的n次方)乘以(x-B的n次方)的橢圓曲線,不可能是模曲線。儘管他努力了,但他的命題和“谷山——志村猜想”矛盾,如果能同時證明這兩個命題,根據反證法就可以知道“費馬大定理”不成立,這一假定是錯誤的,從而就證明了“費馬大定理”。但當時他沒有嚴格證明他的命題。
弗雷命題
1986年,美國數學家裡貝特證明了弗雷命題,於是希望便集中於“谷山——志村猜想”。
完成證明
1993年6月,英國數學家懷爾斯證明了:對有理數域上的一大類橢圓曲線,“谷山——志村猜想”成立。由於他在報告中表明了弗雷曲線恰好屬於他所說的這一大類橢圓曲線,也就表明了他最終證明了“費馬大定理”;但專家對他的證明審察發現有漏洞,於是,維爾斯又經過了一年多的拼搏,於1994年9月徹底圓滿證明了“費馬大定理”。
四色定理
內容及提出
四色問題的內容是:“任何一張平面地圖只用四種顏色就能使具有共同邊界的國家著上不同的顏色。”用數學語言表示,即“將平面任意地細分為不相重疊的區域,每一個區域總可以用1,2,3,4這四個數字之一來標記,而不會使相鄰的兩個區域得到相同的數字。”
這裡所指的相鄰區域,是指有一整段邊界是公共的。如果兩個區域只相遇於一點或有限多點,就不叫相鄰的。因為用相同的顏色給它們著色不會引起混淆。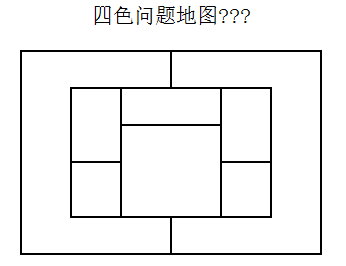 四色猜想
四色猜想
 四色猜想
四色猜想四色猜想的提出來自英國。1852年,畢業於倫敦大學的弗南西斯·格思里來到一家科研單位搞地圖著色工作時,發現了一種有趣的現象:“看來,每幅地圖都可以用四種顏色著色,使得有共同邊界的國家都被著上不同的顏色。”這個現象能不能從數學上加以嚴格證明呢?他和在大學讀書的弟弟格里斯決心試一試。兄弟二人為證明這一問題而使用的稿紙已經堆了一大疊,可是研究工作沒有進展。
求證歷程
1852年10月23日,他的弟弟就這個問題的證明請教了他的老師、著名數學家德·摩爾根,摩爾根也沒有能找到解決這個問題的途徑,於是寫信向自己的好友、著名數學家漢密爾頓爵士請教。漢密爾頓接到摩爾根的信後,對四色問題進行論證。但直到1865年漢密爾頓逝世為止,問題也沒有能夠解決。
1872年,英國當時最著名的數學家凱利正式向倫敦數學學會提出了這個問題,於是四色猜想成了世界數學界關注的問題。世界上許多一流的數學家都紛紛參加了四色猜想的大會戰。1878~1880年兩年間,著名的律師兼數學家肯普和泰勒兩人分別提交了證明四色猜想的論文,宣布證明了四色定理,大家都認為四色猜想從此也就解決了。
肯普的證明是這樣的:首先指出如果沒有一個國家包圍其他國家,或沒有三個以上的國家相遇於一點,這種地圖就說是“正規的”(左圖)。如為正規地圖,否則為非正規地圖(右圖)。一張地圖往往是由正規地圖和非正規地圖聯繫在一起,但非正規地圖所需顏色種數一般不超過正規地圖所需的顏色,如果有一張需要五種顏色的地圖,那就是指它的正規地圖是五色的,要證明四色猜想成立,只要證明不存在一張正規五色地圖就足夠了。
肯普是用歸謬法來證明的,大意是如果有一張正規的五色地圖,就會存在一張國數最少的“極小正規五色地圖”,如果極小正規五色地圖中有一個國家的鄰國數少於六個,就會存在一張國數較少的正規地圖仍為五色的,這樣一來就不會有極小五色地圖的國數,也就不存在正規五色地圖了。這樣肯普就認為他已經證明了“四色問題”,但是後來人們發現他錯了。
不過肯普的證明闡明了兩個重要的概念,對以後問題的解決提供了途徑。第一個概念是“構形”。他證明了在每一張正規地圖中至少有一國具有兩個、三個、四個或五個鄰國,不存在每個國家都有六個或更多個鄰國的正規地圖,也就是說,由兩個鄰國,三個鄰國、四個或五個鄰國組成的一組“構形”是不可避免的,每張地圖至少含有這四種構形中的一個。
肯普提出的另一個概念是“可約”性。“可約”這個詞的使用是來自肯普的論證。他證明了只要五色地圖中有一國具有四個鄰國,就會有國數減少的五色地圖。自從引入“構形”,“可約”概念後,逐步發展了檢查構形以決定是否可約的一些標準方法,能夠尋求可約構形的不可避免組,是證明“四色問題”的重要依據。但要證明大的構形可約,需要檢查大量的細節,這是相當複雜的。
11年後,即1890年,在牛津大學就讀的年僅29歲的赫伍德以自己的精確計算指出了肯普在證明上的漏洞。他指出肯普說沒有極小五色地圖能有一國具有五個鄰國的理由有破綻。不久,泰勒的證明也被人們否定了。人們發現他們實際上證明了一個較弱的命題——五色定理。就是說對地圖著色,用五種顏色就夠了。後來,越來越多的數學家雖然對此絞盡腦汁,但一無所獲。於是,人們開始認識到,這個貌似容易的題目,其實是一個可與費馬猜想相媲美的難題。
進入20世紀以來,科學家們對四色猜想的證明基本上是按照肯普的想法在進行。1913年,美國著名數學家、哈佛大學的伯克霍夫利用肯普的想法,結合自己新的構想;證明了某些大的構形可約。後來美國數學家富蘭克林於1939年證明了22國以下的地圖都可以用四色著色。1950年,有人從22國推進到35國。1960年,有人又證明了39國以下的地圖可以只用四種顏色著色;隨後又推進到了50國。看來這種推進仍然十分緩慢。
資訊時代的成功
高速數字計算機的發明,促使更多數學家對“四色問題”的研究。從1936年就開始研究四色猜想的海克,公開宣稱四色猜想可用尋找可約圖形的不可避免組來證明。他的學生丟雷寫了一個計算程式,海克不僅能用這程式產生的數據來證明構形可約,而且描繪可約構形的方法是從改造地圖成為數學上稱為“對偶”形著手。
他把每個國家的首都標出來,然後把相鄰國家的首都用一條越過邊界的鐵路連線起來,除首都(稱為頂點)及鐵路(稱為弧或邊)外,擦掉其他所有的線,剩下的稱為原圖的對偶圖。到了六十年代後期,海克引進一個類似於在電網路中移動電荷的方法來求構形的不可避免組。在海克的研究中第一次以頗不成熟的形式出現的“放電法”,這對以後關於不可避免組的研究是個關鍵,也是證明四色定理的中心要素。
電子計算機問世以後,由於演算速度迅速提高,加之人機對話的出現,大大加快了對四色猜想證明的進程。美國伊利諾大學哈肯在1970年著手改進“放電過程”,後與阿佩爾合作編制一個很好的程式。就在1976年6月,他們在美國伊利諾斯大學的兩台不同的電子計算機上,用了1200個小時,作了100億判斷,終於完成了四色定理的證明,轟動了世界。
這是一百多年來吸引許多數學家與數學愛好者的大事,當兩位數學家將他們的研究成果發表的時候,當地的郵局在當天發出的所有郵件上都加蓋了“四色足夠”的特製郵戳,以慶祝這一難題獲得解決。
“四色問題”的被證明不僅解決了一個歷時100多年的難題,而且成為數學史上一系列新思維的起點。在“四色問題”的研究過程中,不少新的數學理論隨之產生,也發展了很多數學計算技巧。如將地圖的著色問題化為圖論問題,豐富了圖論的內容。不僅如此,“四色問題”在有效地設計航空班機日程表,設計計算機的編碼程式上都起到了推動作用。
不過不少數學家並不滿足於計算機取得的成就,他們認為應該有一種簡捷明快的書面證明方法。直到現在,仍由不少數學家和數學愛好者在尋找更簡潔的證明方法。
幾何證明
在平面地圖中,為了區分相鄰的圖形,相鄰圖形需要使用不同的顏色來上色,與這兩個相鄰圖形都有鄰邊的圖形需要使用第三種顏色,我們先假設四色定理成立,根據四色定理得出在一個平面內最多有四個互有鄰邊的圖形,而因為第四個與三個互有鄰邊的圖形都有鄰邊的圖形有鄰邊的圖形會包圍一個圖形,所以一個平面內互有鄰邊的圖形最多有四個,所以四色定理成立(互有鄰邊,舉例: 三個互有鄰邊的圖形——A和B有鄰邊 C和AB都有鄰邊)
哥德巴赫猜想
猜想
史上和質數有關的數學猜想中,最著名的當然就是“哥德巴赫猜想”了。
1742年6月7日,德國數學家哥德巴赫在寫給著名數學家歐拉的一封信中,提出了一個大膽的猜想:
任何不小於3的奇數,都可以是三個質數之和(如:7=2+2+3,當時1仍屬於質數)。
同年,6月30日,歐拉在回信中提出了另一個版本的哥德巴赫猜想:
任何偶數,都可以是兩個質數之和(如:4=2+2。當時1仍屬於質數)。
這就是數學史上著名的“哥德巴赫猜想”。顯然,前者是後者的推論。因此,只需證明後者就能證明前者。所以稱前者為弱哥德巴赫猜想(已被證明),後者為強哥德巴赫猜想。由於現在1已經不歸為質數,所以這兩個猜想分別變為
任何不小於7的奇數,都可以寫成三個質數之和的形式;
任何不小於4的偶數,都可以寫成兩個質數之和的形式。
簡述
歐拉在給哥德巴赫的回信中, 明確表示他深信這兩個猜想都是正確的定理,但是歐拉當時還無法給出證明。由於歐拉是當時歐洲最偉大的數學家,他對哥德巴赫猜想的信心,影響到了整個歐洲乃至世界數學界。從那以後,許多數學家都躍躍欲試,甚至一生都致力於證明哥德巴赫猜想。可是直到19世紀末,哥德巴赫猜想的證明也沒有任何進展。證明哥德巴赫猜想的難度,遠遠超出了人們的想像。有的數學家把哥德巴赫猜想比喻為“數學王冠上的明珠”。 猜想手稿
猜想手稿
 猜想手稿
猜想手稿我們從6=3+3、8=3+5、10=5+5、……、100=3+97=11+89=17+83、……這些具體的例子中,可以看出哥德巴赫猜想都是成立的。有人甚至逐一驗證了3300萬以內的所有偶數,竟然沒有一個不符合哥德巴赫猜想的。20世紀,隨著計算機技術的發展,數學家們發現哥德巴赫猜想對於更大的數依然成立。可是自然數是無限的,誰知道會不會在某一個足夠大的偶數上,突然出現哥德巴赫猜想的反例呢?於是人們逐步改變了探究問題的方式。
1900年,20世紀最偉大的數學家希爾伯特,在國際數學會議上把“哥德巴赫猜想”列為23個數學難題之一。此後,20世紀的數學家們在世界範圍內“聯手”進攻“哥德巴赫猜想”堡壘,終於取得了輝煌的成果。
證明進程
20世紀的數學家們研究哥德巴赫猜想所採用的主要方法,是篩法、圓法、密率法和三角和法等等高深的數學方法。解決這個猜想的思路,就像“縮小包圍圈”一樣,逐步逼近最後的結果。
1924年,德國數學家雷德馬赫證明了定理“7+7”。很快,“6+6”、“5+5”、“4+4”和“3+3”逐一被攻陷。1957年,中國數學家王元證明了“2+3”。1962年,中國數學家潘承洞證明了“1+5”,同年又和王元合作證明了“1+4”。1965年,蘇聯數學家證明了“1+3”。
1966年,中國著名數學家陳景潤攻克了“1+2”,也就是:“任何一個足夠大的偶數,都可以表示成兩個數之和,而這兩個數中的一個就是奇質數,另一個則是兩個奇質數的積。”這個定理被世界數學界稱為“陳氏定理”。
由於陳景潤的貢獻,人類距離哥德巴赫猜想的最後結果“1+1”僅有一步之遙了。但為了實現這最後的一步,也許還要歷經一個漫長的探索過程。有許多數學家認為,要想證明“1+1”,必須通過創造新的數學方法,以往的路很可能都是走不通的。

