正文描述了空間上的點的數量與其所構成的邊數量和面數量的關係公式,以及可見邊和可見面與頂點的數量關係的公式。
基本介紹
- 中文名:點邊面公式
- 外文名:Point boundary surface formula
- 套用學科:數學幾何
- 適用領域範圍:數學
定義



公式:
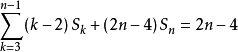
正文描述了空間上的點的數量與其所構成的邊數量和面數量的關係公式,以及可見邊和可見面與頂點的數量關係的公式。



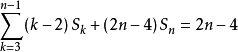
正文描述了空間上的點的數量與其所構成的邊數量和面數量的關係公式,以及可見邊和可見面與頂點的數量關係的公式。...
中點公式是定比分點公式的特例,利用中點公式,已知平面內兩個點的坐標就可以求出它的中點坐標,此外還可解決一類關於某點對稱的問題。...
兩點間距離公式常用於函式圖形內求兩點之間距離、求點的坐標的基本公式,是距離公式之一。兩點間距離公式敘述了點和點之間距離的關係。...
扇形計算公式編輯 鎖定 討論999 一條弧和經過這條弧兩端的兩條半徑所圍成的圖形叫扇形(半圓與直徑的組合也是扇形)。顯然, 它是由圓周的一部分與它所對應的圓心...
面積公式海倫公式 任意三角形的面積公式(海倫公式):S2=p(p-a)(p-b)(p-c), p=(a+b+c)/2, a,b,c為三角形三邊。面積公式坐標公式 ...
倍邊公式是求正多邊形邊長的公式,曾被中外古代數學家用於計算圓周率的近似值。...... 倍邊公式是求正多邊形邊長的公式,曾被中外古代數學家用於計算圓周率的近似值。...
球面半邊公式(formulas of the spherical half side)是球面三角的基本公式之一,即用與球面三角形各角有關的三角函式表示其各邊之半的三角函式的公式。...
圖中的“0”其實不是一個單獨的格點多邊形,而是由兩個格點多邊形複合而成的圖形,故不能直接套用格點公式,需要分開來計算。【正確解法】:外圈的八邊形的邊界格...
定比分點公式一般指有向線段的定比分點的坐標公式,是平面幾何和解析幾何的基本公式。定比分點公式不僅在解析幾何中有十分廣泛的套用,還可以用它解決代數問題,它...
圓柱的表面積:圓柱的表面積等於底面的周長乘高再加上兩頭的圓的面積。...數學公式三角形 15 定理 三角形任意兩邊的和大於第三邊16 推論 三角形任意兩邊...
外接圓半徑公式編輯 鎖定 經過三角形各頂點的圓叫做三角形的外接圓,表示三角形外接圓半徑的方法有:1.用三角形的邊和角來表示它的外接圓的半徑;2.用三角形的三邊...
在數學上,以尤利烏斯·普呂克(JuliusPlücker)命名的普呂克公式是普呂克於20世紀30年代首先開發的一種公式,在曲線和它的對偶函式中,常被稱為“屬”的不變數,與其他...
球面距離公式是計算球面上兩點間距離的公式。設所求...② 緯度:地球上任意一點與地心的連線和赤道面所...此時三角形AOB三條邊都已知,所以∠AOB也可以用餘弦...
正方形面積計算公式(Square area calculation formula)...有一組鄰邊相等的矩形是正方形。 有一個角為直角...“特殊的平行四邊形”易錯點剖析[J]. 國中生世界,...
圓柱的側面積:圓柱的側面積等於底面的周長乘高。S=ch=πdh=2πrh...計算公式三角形 15 定理 三角形任意兩邊的和大於第三邊16 推論 三角形任意兩邊...
交角公式是計算角的一種公式,設點Pi的直角坐標為(xi,yi)(i=0,1,2),則以射線P0P1與P0P2為邊的角θ∈(0,π)可由余弦定理而得。可以從兩向量的夾角思考...
通俗的說是求曲邊三角形的面積,這巧妙的求解方法是...不定積分的積分公式主要有如下幾類:含ax+b的積分...某個區域上的整體性質,改變函式某點的取值不會改變...
布雷特施奈德公式(Bretschneide formula) 設簡單四邊形的四邊為a、b、c、d,兩對角線為e、f,則面積若四邊中有一邊退縮為零,上述公式即成秦九韶公式(三斜求積...
以直角梯形垂直於底邊的腰所在直線為旋轉軸,其餘各邊旋轉而形成的曲面所圍成的...圓台公式 編輯 圓台的體積公式: ,其中r是上底面半徑,R是下底面半徑。...
空間中,到兩點距離相同點的軌跡 解析幾何公式 A*...平面線面平行的判定 平面外的一條直線與此平面內的...邊最多與前面已畫的(n-1)個三角形的各兩條邊...
