普呂克公式是1839年得到的曲線計數幾何中的一組重要公式。
在數學上,以尤利烏斯·普呂克(JuliusPlücker)命名的普呂克公式是普呂克於20世紀30年代首先開發的一種公式,在曲線和它的對偶函式中,常被稱為“屬”的不變數,與其他不變的公式相關聯。不變數稱為曲線及其雙重共同的屬,通過類似的公式連線到其他不變數。這些公式以及每個不變數必須是正整數的事實對其可能的值給予相當嚴格的限制。
基本介紹
- 中文名:普呂克公式
- 外文名:Plücker formula
- 領域:數學
- 命名者:尤利烏斯·普呂克
- 提出時間:1839年
- 相關名詞:普呂克不變數
簡介,普呂克不變數和基本方程,非奇異曲線,曲線類型,
簡介
在數學上,以尤利烏斯·普呂克(JuliusPlücker)命名的普呂克公式是普呂克於20世紀30年代首先開發的一種公式,在曲線和它的對偶函式中,常被稱為“屬”的不變數,與其他不變的公式相關聯。不變數稱為曲線及其雙重共同的屬,通過類似的公式連線到其他不變數。這些公式以及每個不變數必須是正整數的事實對其可能的值給予相當嚴格的限制。
普呂克不變數和基本方程
在此背景下的曲線由複雜射影平面內的非退化代數方程定義。在這個平面上的直線對應於雙投影平面上的點,與給定代數曲線C相切的直線對應於一個代數曲線C中的點,稱為對偶曲線。在射影平面與它的對偶之間的對應關係中,C點對應於切線C *,所以C *的對偶可以與C相結合。
普呂克公式所涵蓋的前兩個不變數是曲線C的d和d *,經典地稱為C類,d是給定的直線與C的交點的次數。(這包括在無窮遠處的複雜點,因為這些曲線是複雜射影平面的子集。)類似地,d *是C的切線的個數,它是通過平面上給定的點的直線;例如,一個圓錐截面有兩個度。如果C沒有奇異點,那么第一個普呂克方程就說明了這一點

但這必須用奇異曲線來修正。
在C的雙點中,讓δ是普通的數字,即具有明顯的切線(這些也稱為節點)或是孤立點,並且令κ為尖點的數量,即具有單切線(spinodes)。 如果C具有較高階奇點,則根據對奇點性質的分析,將它們計算為多重雙點。 例如,普通的三重點被計算為3個雙點。 同樣,複數點和無窮大點都包含在這些計數中。 修正後的形式是第一個普呂克方程式。

類似地,令δ*是普通雙點數,κ*是C *的數量。 然後第二個普呂克方程表示

C *的普通雙點的幾何解釋是在兩點(雙切線)處與曲線相切的線,並且C *的尖點的幾何解釋是拐點(固定切線)。
例如,考慮平滑立方的情況:

上面的公式表明它有

拐點。 如果三次退化並得到一個雙點,則6個點會聚到奇異點,並且只有3個拐點沿奇異曲線保持。 如果立方退化並獲得尖點,則只剩下一個拐點。
請注意,前兩個普呂克方程有雙重版本:


到目前為止,給出的四個方程實際上是依賴的,所以任何三個方程可以用於導出剩餘的。從它們中,給出d,d *,δ,δ*,κ,κ*中的任何三個不變數,可以計算剩餘的三個。
最後,C的屬,經常被定義為:


並且是正整數。
在7個未知數中共有四個獨立的方程,並且與它們中的任何三個這些不變式可用於計算剩餘的四個。
非奇異曲線
一個重要的特殊情況是當曲線C是非奇異的,或者等價地δ和κ是0時,剩下的不變數只能用d來計算。 在這種情況下,結果是:




因此,例如,非奇異四邊形平面曲線屬於3類,具有28個雙切線和24個拐點。
曲線類型
曲線根據其普呂克不變數分類為許多類型。普呂克方程以及普呂克不變數必須都是自然數的限制極大地限制了給定度的曲線的可能類型的數量。投影等效的曲線具有相同的類型,儘管相同類型的曲線通常不是投射等價的。 2級曲線,圓錐截面,具有d=d*= 2給出的單一類型,

對於3級曲線,有三種可能的類型,由下式給出:
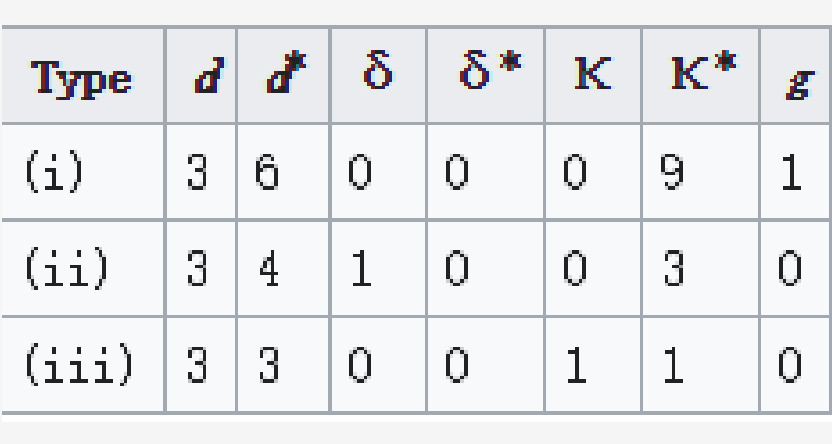
類型(ii)和(iii)的曲線分別是合理的立方體,分別稱為節點和尖端。 類型(i)的曲線是非圓形立方體(橢圓曲線)。
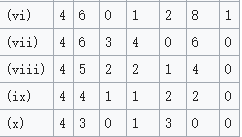
對於4級曲線,有10種可能的類型,由下表給出: