隨機向量分布函式(distribution function ofrandom vector)能完全描述隨機向量機率分布的多元函式。
基本介紹
- 中文名:隨機向量分布函式
- 外文名:distribution function ofrandom vector
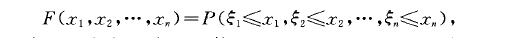
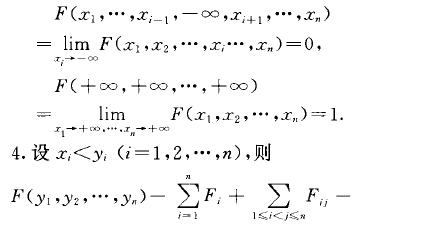
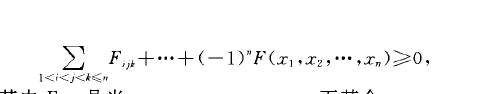
隨機向量分布函式(distribution function ofrandom vector)能完全描述隨機向量機率分布的多元函式。
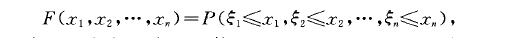
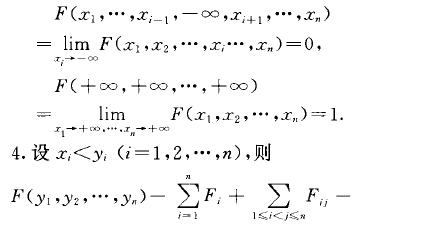
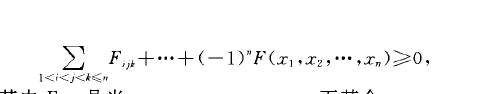
隨機向量分布函式(distribution function ofrandom vector)能完全描述隨機向量機率分布的多元函式。設寧一防1 1 }z , ".. } }n)是定義在機率空間(fl,.} >P)上...
隨機向量由多個隨機變數組成的向量。簡介 隨機向量(random vector)由多個隨機變數組成的向量。 給定樣本空間,如果其上的實值函式 是 (實值)可測函式,則稱 為(實值)隨機變數。初等機率論中通常不涉及到可測性的概念,而直接把任何 的函式稱為隨機變數。如果 指定給機率空間 中每一個事件 有一個...
連續型隨機向量(absolutly continuous randomvector)一類重要的隨機向量。中文名 連續型隨機向量 外文名 absolutly continuous randomvector 所屬學科 數學 如果n維隨機向量寧一傳i } }z,一,之。)的分布函式I',(二,}x2}... }x}})絕對連續,即存在非負可積函式}}xl}x2,"..}x,}),使對一切(x} }x2,...
多項式分布(Multinomial Distribution)是二項式分布的推廣。二項分布的典型例子是扔硬幣,硬幣正面朝上機率為p, 重複扔n次硬幣,k次為正面的機率即為一個二項分布機率。把二項分布公式推廣至多種狀態,就得到了多項分布。定義 如果一個隨機向量X=(X1,X2,…,Xn)滿足下列條件:(1)Xi≥0(1≤i≤n),且X1+...
設xER”是實向量,cw Aw bco和夸。依次是n維隨機向量、nXm隨機矩陣、m維隨機向量和隨機向量,f',·和g(·,·)分別是實值函式和向量函式,對於線性隨機規劃問題(L.SP )和非線性隨機規劃問題(NSP )其分布問題即為求其(隨機)最優值z(w)或最優解zw的機率分布和其他與分布有關量的問題.
稱為連續型隨機向量,稱為連續型分布函式,而 稱為 的分布密度,其分布密度有如下性質:1. 2. 3. 若 在點 處連續,則有 4. 若 是 平面上的一個區域,則點 落在 內的機率為 亦即機率 等於以 為底、以曲面 為頂面的柱體體積。例題解析 例1 設隨機變數X的機率密度為 試求X的分布函式。解: 當 時,...
常態分配 常態分配的密度函式的特點是:關於μ對稱,在μ處達到最大值,在正(負)無窮遠處取值為0,在μ±σ處有拐點。它的形狀是中間高兩邊低,圖像是一條位於x軸上方的鐘形曲線。當μ=0,σ2=1時,稱為標準常態分配,記為N(0,1)。μ維隨機向量具有類似的機率規律時,稱此隨機向量遵從多維常態分配...
李裕發. 一個離散型隨機向量的分布.《VIP》,1994 劉志平. 淺談二維離散型隨機向量(聯合)分布的教學.《CNKI》,1998 高際宇,王桂花. 用表格法求二維離散型隨機向量函式的分布.《CNKI;WanFang》,2006 高際宇,王桂花. 用表格法求二維離散型隨機向量函式的分布.《商丘職業技術學院學報》,2006 查看全部 ...
一維常態分配 若隨機變數 服從一個位置參數為 、尺度參數為 的機率分布,且其機率密度函式為 則這個隨機變數就稱為正態隨機變數,正態隨機變數服從的分布就稱為常態分配,記作 ,讀作 服從 ,或 服從常態分配。μ維隨機向量具有類似的機率規律時,稱此隨機向量遵從多維常態分配。多元常態分配有很好的...
常態分配的密度函式的特點是:關於μ對稱,在μ處達到最大值,在正(負)無窮遠處取值為0,在μ±σ處有拐點。它的形狀是中間高兩邊低,圖像是一條位於x軸上方的鐘形曲線。當μ=0,σ2=1時,稱為標準常態分配,記為N(0,1)。μ維隨機向量具有類似的機率規律時,稱此隨機向量遵從多維常態分配。多元正...
是尺度參數,這樣凡與位置-尺度參數族有關的結果,均對Logistic分布有效。當 時,相應的分布稱為標準Logistic分布,它的分布函式 與分布密度 為 很明顯,如考慮 則 也是一個分布函式,且有關係式 因此有時上也從 出發,以它作為標準分布,經隨機變數線性變換後導出的分布作為一般的Logistic分布。一元logistic函式 一...
有些隨機現象需要同時用多個隨機參數來描述。例如對地面目標射擊,彈著點的位置需要兩個坐標才能確定,因此研究它要同時考慮兩個隨機參數,一般稱同一機率空間(Ω,F,p)上的n個隨機參數構成的n維向量X=(x1,x2,…,xn)為n維隨機向量。隨機參數可以看作一維隨機向量。稱n元x1,x2,…,xn的函式為X的(聯合)分布函...
與矩母函式不同,特徵函式總是存在。如果F是累積分布函式,那么特徵函式由黎曼-斯蒂爾切斯積分給出:如果隨機變數的機率密度函式存在,機率密度函式為,上述積分可以簡化為:其中 是隨機變數X的機率密度函式。如果X是一個向量值隨機變數,我們便取自變數t為向量,tX為數量積。函式性質 特徵函式具有以下基本性質:勒維...
常態分配的密度函式的特點是:關於μ對稱,在μ處達到最大值,在正(負)無窮遠處取值為0,在μ±σ處有拐點。它的形狀是中間高兩邊低,圖像是一條位於x軸上方的鐘形曲線。當μ=0,σ^2=1時,稱為標準常態分配,記為N(0,1)。μ維隨機向量具有類似的機率規律時,稱此隨機向量遵從多維常態分配。多元正...
N維隨機向量 如果服從多變數常態分配,必須滿足下面的三個等價條件:任何線性組合 服從常態分配。存在隨機向量 ( 它的每個元素服從獨立標準常態分配),向量 及 矩陣A滿足 存在 和一個對稱半正定陣 滿足X的特徵函式 如果 是非奇異的,那么該分布可以由以下的PDF來描述: 注意這裡的 表示協方差矩陣...
瑞利分布(Rayleigh Distribution):當一個隨機二維向量的兩個分量呈獨立的、均值為0,有著相同的方差的常態分配時,這個向量的模呈瑞利分布。簡要說明 瑞利分布是最常見的用於描述平坦衰落信號接收包絡或獨立多徑分量接收包絡統計時變特性的一種分布類型。兩個正交高斯噪聲信號之和的包絡服從瑞利分布。瑞利分布的機率...
2.6 隨機變數的數字特徵(50)2.6.1隨機變數的數學期望(50)2.6.2隨機變數函式的數學期望(51)2.6.3隨機變數的方差(52)2.6.4隨機變數的矩和切比雪夫(Chebyshev)不等式(54)習題2(55)第3章 隨機向量的分布及數字特徵(57)3.1 隨機向量的分布(57)3.1.1隨機向量及其分布函式(57)3.1.2二維離散型隨機向量...
cdfplot是繪製經驗累計分布函式圖,顯示了一維向量X的累計機率分布F(x)的圖形。目的是為了觀測隨機變數的取值在哪個附近出現的機率比較大,如果越接近0.5,說明出現的機率越大。使用方法 cdf(x) 繪製累計分布函式圖 H = cdfplot(x) 返回累計分布函式曲線的句柄 [h,stats] = cdfplot(x) 同時返回句柄及統計數據 ...
一、隨機向量函式的數學期望 二、數學期望與方差的運算性質 三、協方差與相關係數 四、隨機向量的數學期望與協方差矩陣 第五章 大數定律與中心極限定理 第一節 大數定律 一、切比雪夫不等式 二、大數定律 第二節 中心極限定理 第六章 樣本與抽樣分布 第一節 總體、樣本與統計量 一、總體 二、樣本 三、統計...
2.5隨機向量函式的分布 習題2 第3章隨機變數的數字特徵 3.1數學期望 3.2矩與方差 3.3協方差及相關係數 習題3 第4章極限定理 4.1極限定理的概念和意義 4.2大數定理和強大數定理 4.3中心極限定理 習題4 第5章數理統計的基本概念 引言 5.1總體和樣本 5.2數據整理與直方圖 5.3抽樣分布與統計量 習題5 ...
3.2邊緣分布 3.3條件分布 3.4隨機變數的獨立性 3.5隨機向量函式的分布 本章小結 總複習題3 第4章隨機變數的數字特徵 4.1數學期望 4.2方差 4.3協方差和相關係數 4.4矩、協方差矩陣 本章小結 總複習題4 第5章大數定律與中心極限定理 5.1切比雪夫不等式 5.2大數定律 5.3中心極限定理 本章小結 總...
第二章 隨機變數及其分布 1.2.1 隨機變數的分布函式 1.2.2 離散型隨機變數 1.2.3 連續型隨機變數 第三章 多維隨機變數的分布 1.3.1 聯合分布的一般性質 1.3.2 多元常態分配 1.3.3 隨機變數的獨立性 1.3.4 隨機向量函式的分布 第四章 隨機變數的數字特徵 1.4.1 一般性質 1.4.2 機率論中...
4.2.1 邊緣分布與條件分布的概念 174 4.2.2 離散型場合 175 4.2.3 連續型場合: 邊緣分布與邊緣密度 180 4.2.4 連續型場合: 條件分布與條件密度 181 4.2.5 隨機變數的獨立性 184 4.3 常見的多維連續型分布 190 4.3.1 多維均勻分布 190 4.3.2 二維常態分配 191 4.4 隨機向量的函式 193 4....
§3?3二維連續型隨機變數及其分布 3?3?1二維連續型隨機變數的聯合機率密度 3?3?2二維連續型隨機變數的邊緣機率密度 3?3?3常用多維連續分布 §3?4隨機變數的獨立性 §3?5條件分布 3?5?1離散型隨機變數的條件分布 3?5?2連續型隨機變數的條件分布 §3?6隨機向量函式的分布 3?6?1離散型隨機向量函式的分布...
第三節 隨機變數的獨立性 第四節 二維隨機向量函式的分布 一、二維離散型隨機向量函式的分布 二、二維連續型隨機向量函式的分布 習題三 第四章 隨機變數的數字特徵 第一節 數學期望 一、數學期望的定義 二、常見分布的數學期望- 三、隨機變數函式的數學期望 四、數學期望的性質 第二節 方差與矩 一、方差的定義...
§3.2 條件分布(62)§3.3 隨機變數的獨立性(66)§3.4 隨機向量函式的分布(70)習題三(77)第4章 隨機變數的數字特徵(81)§4.1 數學期望(81)§4.2 方差(87)§4.3 協方差與相關係數(92)§4.4 大數定律與中心極限定理(97)習題四(104)第5章 數理統計的基礎知識(108)§5.1 數理...
3.1 n維隨機向量及其分布函式 3.2 二維隨機變數及其分布 3.3 邊緣分布 3.4 條件分布 3.5 隨機變數的獨立性 3.6 二維隨機變數函式的分布 習題3 第4章 數字特徵 4.1 數學期望 4.2 方差 4.3 隨機向量的數字特徵 4.4 矩 習題4 第5章 大數定律和中心極限定理 5.1 大數定律 5.2 中心極限定理 習題...
3.2 邊緣分布 /42 3.3 條件分布 /45 3.4 隨機變數的獨立性 /49 3.5 隨機向量函式的分布 /51 總複習題3 /53 第4章 隨機變數的數字特徵 /63 4.1 數學期望 /63 4.2 方差 /67 4.3 協方差和相關係數 /69 4.4 矩、協方差矩陣 /71 總複習題4 /72 第5章 大數定律與中心極限定理 /79...
4.4 常見分布的期望 4.5 大數定律 第五章 連續型隨機變數 5.1 可測性 5.2 分布函式的實現 5.3 密度函式 第六章 隨機向量 6.1 隨機向量及聯合分布 6.2 均勻分布與常態分配 6.3 隨機向量的函式的分布 第七章 隨機序列的收斂 7.1 收斂的不同意義 7.2 強大數定律 7.3 Kolmogorov不等式與強大數...
3.7隨機向量函式的分布 64 3.7.1Z=X+Y的分布 64 3.7.2Z=max{X,Y}和Z=min{X,Y}的分布 66 3.8n維隨機向量 68 3.8.1定義和分布函式 69 3.8.2n維連續型隨機向量 69 3.8.3n維隨機向量函式的分布 70 習題3 71 第4章隨機變數的數字特徵 75 4.1數學期望 75 4.1.1離散型隨機變數的數學期望 ...
