基本介紹
由來
簡介
定義
公式
表達式

參數定義
圖形特徵


常態分配密度曲線反映了隨機變數的分布規律。理論上的常態分配曲線是一條中間高,兩端逐漸下降且完全對稱的鐘形曲線。由來常態分配曲線是指滿足常態分配的分布曲線。而常態分配(Normal distribution),也稱“常態分...
正態曲線呈鐘型,兩頭低,中間高,左右對稱因其曲線呈鐘形,因此人們又經常稱之為鐘形曲線。若隨機變數X服從一個數學期望為μ、方差為σ²的常態分配,記為N(μ,σ²)。其機率密度函式為常態分配的期望值μ決定了其位置,其標準差σ決定了分布的幅度。當μ = 0,σ = 1時的常態分配是標準常態分配。...
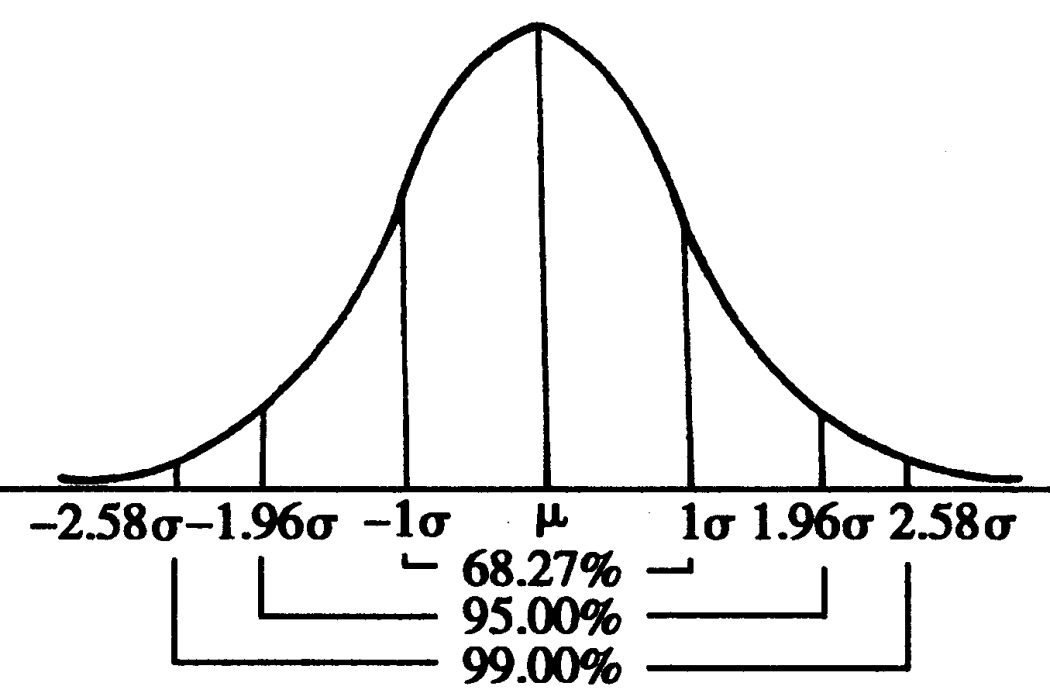
常態分配的機率密度函式曲線呈鐘形,因此人們又經常稱之為鐘形曲線。我們通常所說的標準常態分配是位置參數均數為0, 尺度參數:標準差為1的常態分配(見圖1中綠色曲線)。特點 密度函式關於平均值對稱 平均值與它的眾數(statistical mode)以及中位數(median)同一數值。函式曲線下68.268949%的面積在平均數左右...
正態曲線 正態曲線是2014年公布的心理學名詞。 定義 常態分配的機率密度函式的圖形。其特徵是“鐘”形曲線。 出處 《心理學名詞》。
頻率曲線(frequency curve):把水文變數和頻率表達成一定的數學關係式並將它繪成圖形,即為頻率曲線。水文統計計算中常用的機率分布曲線有常態分配和皮爾遜Ⅲ型曲線。常態分配的密度函式為f(x)=1σ2πe-(x-x)2[]2σ2。式中:σ為均方差;e為自然對數的底。常態分配的特性,在誤差估算中常被套用。皮爾遜Ⅲ...
1.以0為中心,左右對稱的單峰分布;2.t分布是一簇曲線,其形態變化與n(確切地說與自由度df)大小有關。自由度df越小,t分布曲線越低平;自由度df越大,t分布曲線越接近標準常態分配(u分布)曲線,如圖:t(n)分布與標準正態N(0,1)的密度函式。3.隨著自由度逐漸增大,t分布逐漸接近標準常態分配。對應於...
在點x處的機率分布密度,簡稱分布密度,記作 分布密度的圖形 通常叫做“分布曲線”。密度函式的性質 連續型分布是隨機變數的兩個常用的分布類型之一,它的分布函式不能用列表方式表示,若隨機變數ξ可取某個區間(c,d)中的一切值,且存在一個非負可積函式 ,使得ξ的分布函式 可以表示為 則稱ξ服從連續型分布,...
具有密度函式 其中 為常數,且 ,則稱 服從參數為 的拉普拉斯分布。易見, ,且 ,(令 ) = .可見 確定了一個密度函式,此外 .如圖1給出了拉普拉斯分布的密度曲線( )。拉普拉斯分布的若干性質 . (1)則稱X服從參數為 (位置參數)和 (尺度參數)的拉普拉斯(Laplace)分布,記作 ...
相對常態分配而言,將不遵從常態分配的其他類型的分布統稱為非常態分配。論述 1、在實際遇到的許多隨機現象都服從或近似服從常態分配。當樣本頻率分布直方圖就無限接近於一條總體密度曲線,總體密度曲線較科學地反映了總體分布。但總體密度曲線的相關知識較為抽象,學生不易理解,因此在總體分布研究中我們選擇常態分配...
分布趨近於常態分配;卡方分布密度曲線下的面積都是1. 2. 分布的均值與方差可以看出,隨著自由度 的增大,χ2分布向正無窮方向延伸(因為均值 越來越大),分布曲線也越來越低闊(因為方差 越來越大)。 3.不同的自由度決定不同的卡方分布,自由度越小,分布越偏斜。 4. 若 互相獨立,則: 服從 分布,自由度為 ; ...
峰度(peakedness;kurtosis)又稱峰態係數。表征機率密度分布曲線在平均值處峰值高低的特徵數。直觀看來,峰度反映了峰部的尖度。樣本的峰度是和常態分配相比較而言統計量,如果峰度大於三,峰的形狀比較尖,比常態分配峰要陡峭。反之亦然。在統計學中,峰度(Kurtosis)衡量實數隨機變數機率分布的峰態。峰度高就意味...
行車速度的統計分布特徵 行車速度與交通量一樣,也是一個隨機變數。研究表明,在鄉村公路和高速公路路段上,運行車速一般呈常態分配,在城市道路或高速公路匝道口處,車速分布比較集中,一般呈偏態分布,如皮爾遜Ⅲ型分布對行車速度進行統計分析,一般要藉助車速分布直方圖和車速頻率累計頻率分布曲線。行車速度的統計分布...
的機率分布,記為:則其機率密度函式為 常態分配的數學期望值或期望值 等於位置參數,決定了分布的位置;其方差 的開平方或標準差 等於尺度參數,決定了分布的幅度。常態分配的機率密度函式曲線呈鐘形,因此人們又經常稱之為鐘形曲線(類似於寺廟裡的大鐘,因此得名)。我們通常所說的標準常態分配是位置參數 ,...
比如圖像處理中最常用的濾波器類型為Gaussian濾波器(也就是所謂的常態分配函式)。數學表達 滿足下述的機率密度分布的隨機變數分布叫做二維常態分配 其中 都是常數,我們稱 服從參數為 的二維常態分配,常把這個分布記作 )。 的範圍分別為 。這個函式在三維空間中的圖像是一個橢圓切面的鐘倒扣在 平面...
GMM,高斯混合模型,也可以簡寫為MOG。高斯模型就是用高斯機率密度函式(常態分配曲線)精確地量化事物,將一個事物分解為若干的基於高斯機率密度函式(常態分配曲線)形成的模型。GMMs已經在數值逼近、語音識別、圖像分類、圖像去噪、圖像重構、故障診斷、視頻分析、郵件過濾、密度估計、目標識別與跟蹤等領域取得了良好的...
EXCEL中的NORMDIST是指返回指定平均值和標準偏差的常態分配函式。此函式在統計方面套用範圍廣泛(包括假設檢驗)。簡介 能建立起一定數據頻率分布直方與該數據平均值和標準差所確定的常態分配數據的對照關係。如圖1所示一批數據的頻率直方圖,曲線是以該批數據平均值和標準差所確定的常態分配曲線。這樣就可知這批數據的...
高斯這項工作對後世的影響極大,它使常態分配同時有了“高斯分布”的名稱,且如第七章曾指出的,後世之所以多將最小二乘法的發明權歸之於他,也是出於這一工作。高斯是一個偉大的數學家,重要的貢獻不勝枚舉。但現今德國10馬克的印有高斯頭像的鈔票,其上還印有常態分配的密度曲線。這傳達了一種想法:在高斯...
univariate過程和以上兩個過程的格式非常相似,相同的語句和選項其含義也相同,所不同的是某些統計量只能在univariate過程中計算(如眾數),以及univariate過程中所具有的繪圖功能。histogram語句即用來指示SAS對其後所指定的變數繪製直方圖,其後的選項用來指示SAS添加不同類型的擬合圖形(如常態分配的分布密度曲線)。tabula...
7.4二項分布與超幾何分布 核心例題1二項分布及分布列 核心例題2二項分布的均值與方差 核心例題3超幾何分布及分布列 核心例題4超幾何分布的均值與方差 7.5常態分配 核心例題1常態分配密度曲線 核心例題2利用正態曲線的對稱性求機率 核心例題3常態分配特殊區間的機率 核心例題4利用3σ原則做決策 微專題3機率常見...
設x被二值化後的取值為xₗ和x₂,Y為等距變數,二列相關係數計算公式為,式中為X=X₁時Y的平均值;為X=X₂時y的平均值;S為Y的標準差;p為X=X₁的樣品個數占全部樣品個數的比例;yp為標準常態分配在p分位點Zₚ處密度曲線的高度。
5.3.2 二項分布機率的計算 5.4 泊松分布 【本章習題】第6章 連續型變數的機率分布 【學習要點】【導讀案例】 多少家庭的電費會漲價 6.1 均勻分布 6.1.1 均勻分布的圖示與特點 6.1.2 均勻分布隨機變數的期望值與標準差 6.2 常態分配 6.2.1 常態分配的機率密度曲線及其特點 6.2.2 標準常態分配...
二項分布 超幾何分布 常態分配 x2分布 t分布 F分布 Poisson分布 負二項分布 均勻分布 圓形分布 伽瑪分布 柯西分布 威布爾分布 指數分布 附錄一 統計用表 附表1 標準常態分配密度函式曲線下離差“左側的面積 附表2 t界值表 附表3 x2分布界值表 附表4 二項分布表 附表5—1 F界值表(方差分析用,P=0.05...
第四章 主要離散分布 第一節 理論分布的意義 第二節 二項分布 第三節 泊松(pOissOn)分布 第四節 其他離散型分布 第五章 主要連續分布——常態分配 第一節 常態分配的意義和函式式 第二節 常態分配密度函式的推導 第三節 正態密度函式的性質 第四節 常態分配曲線的圖示和機率積分 第五節 常態分配的期望...
為單一高斯機率密度函式的延伸,用多個高斯機率密度函式(常態分配曲線)精確地量化變數分布,是將變數分布分解為若干基於高斯機率密度函式(常態分配曲線)分布的統計模型。隱馬爾可夫模型 隱馬爾可夫模型(Hidden Markov Model,HMM)是統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中...
表征機率分布密度曲線相對於平均值不對稱程度的特徵數。直觀看來就是密度函式曲線尾部的相對長度。定義上偏度是樣本的三階標準化矩,定義式如下,其中 分別表示二階和三階中心矩:常態分配的偏度為0,兩側尾部長度對稱。若以bs表示偏度。bs0稱分布具有正偏離,也稱右偏態,此時數據位於均值右邊的比位於左邊的少,...
