基本介紹
- 中文名:里斯定理
- 外文名:Riesz representation theorem
希爾伯特空間表示定理
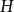
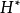
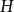
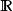
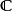

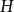
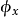
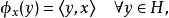
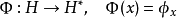


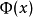
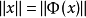
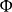
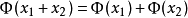
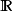
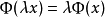
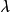
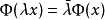

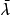
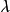
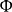
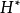
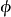
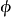
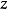
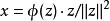
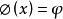
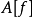
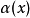
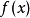
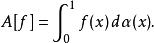
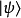
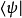
Cc(X) 上線性泛函的表示定理
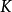
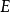
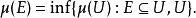
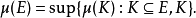
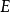
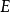
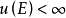
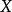
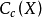
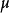

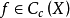
C0(X) 的對偶空間的表示定理
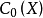
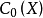
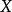
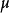
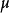
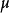
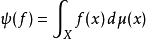
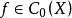
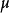
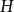
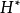
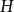
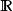
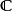

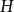
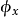
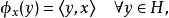
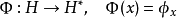


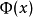
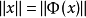
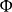
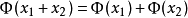
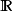
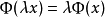
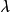
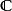
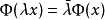

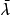
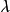
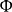
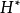
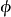
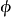
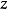
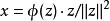
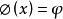
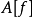
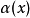
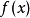
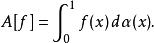
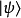
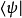
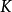
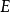
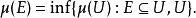
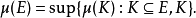
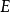
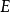
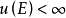
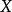
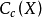
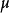

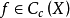
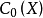
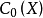
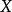
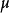
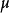
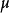
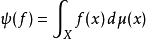
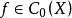
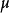
在泛函分析中,有多個有名的定理冠以里斯定理,又稱里斯表示定理(Riesz representation theorem),它們是為了紀念匈牙利數學家弗里傑什·里斯。...
這個定理建立了希爾伯特空間與它的對偶空間的一個重要聯繫:如果底域是實數,兩者是等距同構;如果域是複數,兩者是等距反同構。在泛函分析中有多個有名的定理冠以里斯...
里斯-費希爾定理是貝塞爾不等式的逆命題。貝塞爾不等式表明:{ck}為L2[a,b]中某個函式的傅立葉係數的必要條件是{ck}2的和函式收斂,里斯-費希爾定理表明這個條件...
里斯分解定理是位勢論中的重要定理。一個上(下)調和函式可表示成調和函式與位勢之和(差)的形式,這種表示法稱為里斯分解。...
里斯引理(Riesz lemma)揭示閉子空間與單位球面上某點的距離性質的重要引理。...... 里斯引理揭示閉子空間與單位球面上某點...考特曼的這一定理在巴拿赫空間局部理論...
里斯-菲舍爾定理是貝塞爾不等式的逆命題,里斯(Riesz,F.)和菲舍爾(Fischer,E.S.)於1907年最早對特殊的希爾伯特空間L2[0, 2π]和規範正交系證明了這個定理。...
里斯(1880~1956)Riesz,Frigyes Frdric,匈牙利數學家。泛函分析創始人之一,又譯黎茲。...
里斯一蘇士凱維奇定理(Rees-Suschkitz theo-rem)描述緊緻半群的核的結構的定理。...... 里斯一蘇士凱維奇定理[1] (Rees-Suschkitz theo-rem)描述緊緻半群的核...
舍恩定理是指對事業懷有信心,相信自己,乃是獲得成功不可或缺的前提。當然其他因素也非常重要,但最基本的條件,是激勵自己達到所希望的目標的積極態度。懷有信念的...
拉克斯-米爾格拉姆定理是數學泛函分析的定理,以彼得·拉克斯和阿瑟·米爾格拉姆命名。這定理可用來藉弱形式求解偏微分方程,因此主要用作有限元法的理論基礎。...
弗里傑什·里斯Frigyes Riesz(1880.1.22,奧地利-匈牙利傑爾〔今匈牙利境內〕~1956.2.28,匈牙利布達佩斯) 匈牙利數學家,在數學物理中有重要套用的泛函分析的開拓者...
埃瓦里斯·迦羅瓦 (Evariste Galois)(1811-1832)迦羅瓦生於公元1811年10月25日,是一個大動亂的時代,當時法國皇帝拿破崙正值權力的顛峰,但是接下來的一年,發生俄國...
《黑洞不是黑的-霍金BBC里斯講演》是2017年6月湖南科學技術出版社出版發行的圖書,作者是 [英]史蒂芬·霍金...
傅立葉變換的限制定理(restriction theorem ofthe Fourier transform)傅立葉變換大小的一種描述,是研究多元函式傅立葉積分的博赫納一里斯平均L0收斂的重要工具.設S...
定位理論,由美國著名行銷專家艾·里斯(Al Ries)與傑克·特勞特(Jack Trout)於20世紀70年代提出。里斯和特勞特認為,定位要從一個產品開始,那產品可能是一種商品、...
上述定理是弗雷德霍姆(Fredholm,E.I.)通過積分方程與線性代數方程組類比的方法(...這一推廣就是泛函分析中里斯-紹德爾理論,它分別由里斯(Riesz,F.)和紹德爾(...
帕塞瓦爾恆等式的這種推廣形式可以用里斯-費歇爾定理加以證明。 [4] 帕塞瓦爾恆等式定理介紹 編輯 畢達哥拉斯定理也叫做勾股定理,是一個基本的幾何定理,指直角三角...
無毛定理意味著宇宙(包括可見和不可見宇宙)在暴脹階段以極為巨大的比例膨脹。當...然而有宇宙學家卻對此表示懷疑,如馬丁·里斯所說:“對於懷疑奇異物理學的人來...
引進了上(下)調和函式的概念,為位勢論研究提供了新的方法;里斯分解定理建立了上調和函式與位勢之間的緊密聯繫;而對上調和函式連續性的研究導致了細拓撲概念的引入...
品牌延伸定律: 里斯夥伴主席、定位之父艾.里斯及傑克.特勞特在行銷實戰中總結出品牌延伸的規則: 1) 當競爭對手中沒有專家品牌的時候,品牌延伸通常不會導致失敗; ...
