里斯分解定理

里斯分解定理是位勢論中的重要定理。一個上（下）調和函式可表示成調和函式與位勢之和（差）的形式，這種表示法稱為里斯分解。

基本介紹

• 中文名：里斯分解定理
• 外文名：Riesz decomposition tueorem 
• 適用範圍：數理科學

簡介

里斯分解定理是位勢論中的重要定理。

一個上（下）調和函式可表示成調和函式與位勢之和（差）的形式，這種表示法稱為里斯分解。關於一種位勢，這種分解的準確表述為：函式f在區域D(D⊂Rⁿ)內上調和的充分必要條件是存在惟一的、集中在D的測度μ≥0（稱為f的對應測度），使得對任何相對緊的區域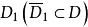，有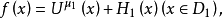

其中μ₁為μ在D₁的限制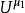，為對數位勢（n=2）或牛頓位勢（n≥3）；H₁在D₁內調和。

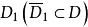
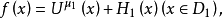
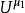
推廣

上式公式中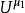也可取作以D₁的格林函式G₁(x,y)為核的位勢

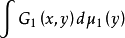這時H₁就是f在D₁的最大調和下屬。

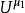
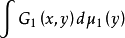
此外，f的對應測度μ實質上就是把f看做廣義函式時，m△f所表示的測度，其中m<0為實常數；特別地，對牛頓位勢，m=-1/4π²。

位勢論

位勢論是數學的一支，它可以定義為調和函式的研究。

“位勢論”一詞的來源在於，在19世紀的物理學中，自然界的基本力被相信為從滿足拉普拉斯方程的位勢導出。因此，位勢論研究可以作為位勢的函式。今天，我們知道自然界更為複雜——表述力的方程可以是諸如愛因斯坦場方程或者楊－米爾斯方程這樣的非線性偏微分方程的系統，而拉普拉斯方程只是在受限情況下的近似。但是，“位勢論”一詞還是保留了作為對滿足拉普拉斯方程的函式的研究的方便叫法。