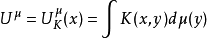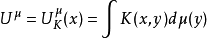對數位勢(logarithmic potential)是一般位勢的經典模型之一。對數核是對稱的、平移不變的，但不是正核。二維引力場的位勢即為對數位勢。
位勢是位勢論的基本概念。所謂位勢，通常指某個函式(核)確定的參變數積分。
基本介紹
- 中文名：對數位勢
- 外文名：logarithmic potential
- 領域：數學
- 學科：位勢論
- 性質：一般位勢的經典模型之一
- 特點：對稱、平移不變
概念,位勢,位勢論,核,一般位勢,
概念
對數位勢(logarithmic potential)是一般位勢的經典模型之一。在R2中，以K(x，y)=-log|x-y|為核(稱為對數核)的位勢稱為對數位勢，記為Uμl。對數核是對稱的、平移不變的，但不是正核。二維引力場的位勢即為對數位勢。
位勢
位勢是位勢論的基本概念。所謂位勢，通常指某個函式(核)確定的參變數積分。產生位勢概念的原型是力學中的引力位勢，即一個梯度場(引力場)的參變數積分，一般在Rn(n≥2)中，由公式：
給出向量場時，函式u=u(x1，x2，…，xn)稱為位勢。此概念現已大大發展，除了常指一般位勢外，還有相應於廣義形式核的位勢，在調和空間用上調和函式定義的無顯示核的位勢，在鞅論中用上鞅定義的位勢等。
位勢論
現代分析數學領域的一個分支，主要研究各種形式的位勢(函式)和與其密切關聯的調和函式、上(下、超、次)調和函式族的各種性質及其套用。經典位勢論的主要研究工具是微積分，並與微分方程、複變函數論緊密關聯；現代位勢論以拓撲、泛函分析與測度論、廣義函式等為主要工具，與分析數學領域的諸多分支相互滲透並和隨機過程建立了深刻的內在聯繫。位勢論起源於物理學的萬有引力學說和靜電學，遠在1733年，拉格朗日(Lagrange，J.-L.)就注意到引力場是一個函式(稱為牛頓位勢)的梯度。在三維歐氏空間，一個單位質點εy的引力場在點x(x≠y)的牛頓位勢等於把一個單位質點從無窮遠移到點x所做的功，其值是1/|x-y|。因此，一個質量分布μ的引力場在x的牛頓位勢是：
1772年，拉普拉斯(Laplace，P.-S.)證明了，在不分布質量的地方，位勢滿足拉普拉斯方程。這樣，物理問題便化為求解偏微分方程的數學問題。
從18世紀到19世紀末，位勢論的研究限於n維歐氏空間上的牛頓位勢(n≥3)和對數位勢(n=2)，即所謂經典位勢論。其中心問題之一是古典狄利克雷問題的求解。1823年，泊松(Poisson，S.-D.)就球域情形給出了解的積分公式；1828年，格林(Green，G.)對邊界充分光滑的有界區域，從物理直觀出發並藉助于格林函式給出了解；1840年，高斯(Gauss，C.F.)採用變分法解決了平衡問題並得出狄氏問題的新解法。這兩個問題與掃除問題相關聯，此後一直被稱為位勢論三大基本問題。1855年，狄利克雷(Dirichlet，P.G.L.)和黎曼(Riemann，(G.F.)B.)利用所謂狄利克雷原理給出了解。此外，還有龐加萊(Poincaré，(J.-)H.)的掃除法，施瓦茲(Schwarz，H.A.)的交錯法等。但是，由於缺乏足夠的數學工具，這些解法是不嚴密的，需要附加條件。另外，在這一時期的主要成果還有：1839年，埃恩蘇(Earnshaw，E.)證明狄氏解的極值原理；1850年，黎曼把位勢論與函式論作統一處理，揭示了格林函式和位勢同保形映射之間的密切聯繫；1886年，哈納克(Harnack，C.G.A.)建立哈納克不等式及哈納克收斂原理。此外，關於諾伊曼問題及多重調和函式的研究也有不少成果。這樣，直到19世紀末，位勢論的三個基本原理，即極小值原理、收斂性質及狄利克雷問題的可解性已基本建立，它為現代位勢論的發展作了很好的準備。
20世紀以來，由於深入套用現代函式論、測度和積分的理論、泛函分析、一般拓撲學、抽象代數、現代機率論的思想和方法，位勢論得到蓬勃發展，開闢了新的研究方向，創造了新的方法，成為分析數學領域中比較徹底完成了現代化變革的一個分支，也影響了其他數學分支的發展。
20世紀初，一個重要發現是，1909年，扎雷姆巴(Zaremba，S.)所揭示的去心球體的經典的狄利克雷問題未必可解這一事實。1913年，由勒貝格(Lebesgue，H.L.)利用所謂勒貝格刺給出的不可解區域的反例更有深刻意義，這導致了對區域邊界非正則點的研究和廣義狄利克雷問題的提出，前者由凱洛格(Kellogg，O.D.)、布利岡(Bouligund，G.L.)、維納(Wiener，N.)等人完全解決；而佩龍(Perron，O.)於1923年提出了關於一般區域的廣義狄利克雷問題並給出新的解法，經過維納(1925年)，特別是布雷洛(Brélot，M.E.)(1939年)的改進和推廣，得到解的存在和惟一性定理的一般形式。此外，柯爾荻希(Keldysh，M.V.)等人在20世紀30年代還研究了狄利克雷問題的解的穩定性。
1925年，里斯(Riesz，F.)引進了上(下)調和函式的概念，為位勢論研究提供了新的方法；里斯分解定理建立了上調和函式與位勢之間的緊密聯繫；而對上調和函式連續性的研究導致了細拓撲概念的引入。
20世紀30年代，瓦萊·普桑(Vallée-Poussin，C.-J.-G.-N.de la)用現代觀點改進並發展了龐加萊掃除法；弗羅斯特曼(Frostman，O.)發展了高斯變分法，成功地解決了緊集的平衡問題和掃除問題。同期，位勢論已推廣到非古典核的情況，特別是里斯位勢核，它已不屬於通常與偏微分方程關聯的位勢核了。
從20世紀40年代起，泛函分析、拓撲學的方法被系統地引入位勢論並使它發展到一個新水平。1941年，嘉當(Cartan，H.)利用希爾伯特空間理論研究具有有限能量的測度等，得到很大成功；同年，馬丁(Martin，R.S.)建立了馬丁邊界理論，導致了關於一般理想邊界的深入研究；1950年，戴尼(Deny，J.)用廣義函式論解決了完備化問題;1955年，紹凱(Choquet，G.)建立了一般容量理論及可容性定理，並用凸錐極端點理論改進了馬丁的成果。此外，對於更一般空間(例如流形、LCA群)和更一般位勢核的位勢論也有了深入的探討。
近30多年來，位勢論迅速發展，其顯著特點之一是各種公理體系的建立。為統一處理已有的理論並加以推廣使之適用於一般橢圓型和拋物型方程或隨機過程，自20世紀50年代中期起，陶茨(Tautz，G.)、杜布(Doob，J.L.)、布雷洛、鮑爾(Bauer，H.)、邦尼(Bony，J.M.)、康斯坦丁斯庫(Constantinescu，C.)和柯尼(Cornea，A.)等人分別提出了不同的公理系統，建立各種形式的調和空間位勢論(最近，關於多重調和空間及非線性位勢論的公理系統也先後建立起來)；而戴尼和博靈(Beurling，A.)等人則從能量和狄利克雷積分等概念出發建立了狄利克雷空間論。位勢論發展的另一個顯著特點是，越來越廣泛深入地與相鄰分支，如複分析(包括黎曼曲面)、拓撲學、幾何測度論、微分幾何、微分方程、調和分析等相互結合和滲透，且發揮日益明顯的作用與影響。特別引人注目的是，對於它與隨機過程論之深刻聯繫的深入研究，同時促進了這兩個分支的繁榮和發展，在杜布、亨特(Hunt，G.A.)、邁耶(Meyer，P.A.)和鐘開萊等人出色工作的基礎上，產生了所謂機率位勢論或馬爾可夫過程位勢論，與此有關的課題正吸引著大批學者去做深入研究。
核
位勢論的基本概念。在位勢論中，所謂核，常指一般位勢的核(參見“一般位勢”)。這時若K(x，y)≥0恆成立，則稱K為正核；令K′(x，y)=K(y，x)(K′稱為K的轉置核)，若K′=K，則稱K為對稱核；當Ω為阿貝爾群且有K(x，y)=K(x-y)時，則稱K為平移不變核；若對於任意有緊支集的μ，有：
則稱K為正定核。此外，還有各種廣義形式的核，如測度核、廣義函式核等。
一般位勢
經典位勢的一種直接推廣形式，常為一個二元數值函式(核)關於某個測度的積分。對於一個取定的核，考慮諸測度所確定的位勢及有關的調和、上(下)調和函式等的性質及其套用的理論稱為關於該核的一般位勢論。設(Ω，F)是一個可測空間，K(x，y)是從Ω×Ω到[-∞，+∞]的可測函式，μ是F上的實測度。若對每個x∈Ω，下式中的積分有意義，則由Ω到[-∞，+∞]的函式：
稱為μ以K為核的一般位勢，簡稱位勢。通常考慮上述Ω同時為局部緊豪斯多夫空間，核K為不取-∞值的下半連續函式，μ為拉東測度(有時設μ≥0，即μ為正測度)。
