基本介紹
- 中文名:邊界對應定理
- 外文名:theorem of boundary correspondence
- 所屬學科:數學
- 屬性:複變函數幾何理論的基本定理之一
- 所屬問題:複變函數論(幾何函式論)
- 相關概念:共形映射,有界單連通區域等
基本介紹








邊界對應定理的逆定理



















































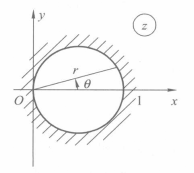
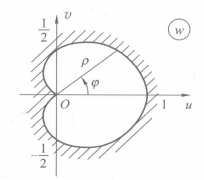






























































邊界對應定理(theorem of boundary correspondence)是複變函數幾何理論的基本定理之一。設z平面上單連通區域D的邊界是一條閉簡單連續曲線C,設單葉函式w=f(z)把D映射成單位圓|w|<...
邊界層定理是當流體在大雷諾數條件下運動時,可把流體的粘性和導熱看成集中作用在流體表面的薄層即邊界層內。根據邊界層的這一特點,簡化納維-斯托克斯方程,並加以求解,即可得到阻力和傳熱規律。這一理論是德國物理學家提出的,它為粘性...
普夫邊界點定理,是有關二階橢圓型方程的一個重要性質。這方程(或不等式)的非常數解在達到最大值的邊界上的外法嚮導數必為正值。設u在區域Ω中滿足不 等式 L在Ω中是一致橢圓型的,假設在Ω中u≤M,在邊 界點P上u=M,且P...
在黎曼映射定理提出之後,C. 卡拉西奧多里證明了邊界對應定理,即在黎曼映射定理的條件下 ,若бD= L是一條簡單閉曲線,則映射函式f (Z) 可以連續開拓到L上且實現L與|w|=1之間的雙方單值連續映射。
13表示定理與相似原理 13.1整體同胚解的表示定理 13.2Beltrami方程解的相似原理 13.3邊界對應定理及唯一性定理 13.4擬共形映射的Holder連續性 13.5擬共形延拓 13.6擬共形映射的Riemann映射定理 13.7全平面上具有給定復特徵的擬共形...
亨特-惠登定理是函式在某點的非切向邊界值與半細邊界值之間的關係的定理。簡介 亨特-惠登定理是函式在某點的非切向邊界值與半細邊界值之間的關係的定理。該定理斷言:李普希茨區域上定義的任何函式若在x₀∈∂D有非切向邊界值,則...
邊界檢驗(boundary verification)是多項式參數空間或係數空間中幾何體穩定性的檢驗方法。其穩定性可由其相對邊界的穩定性所保證.邊界檢驗一般要求參數到多項式係數的映射為仿射映射.關於邊界檢驗的主要結果有邊界定理和原象定理.邊界定理是...
第二章 恆壓相圖的邊界理論——相區及其邊界構成相圖的規律 2·1引言 2·2相圖中的幾個基本概念——特別是相邊界的概念 2·3相圖中的對應關係定理及其與相律的關係 2·4對應關係定理在恆壓相圖中的推論——恆壓相圖中φ、R1和ф...
法圖-杜布定理是關於細邊界值存在性的定理。經典的法圖定理斷言:Rⁿ的球內的正調和函式在邊界上幾乎處處有非切向邊界值。杜布(Doob,J.L.)將它推廣為,關於格林區域D附加其馬丁邊界△所得的緊空間上的細拓撲,D內的上調和函式u>...
羅伯津斯基定理的一個套用是說明要素積累對生產可能性邊界的影響效果。封閉條件下 要素稟賦增加之後,生產可能性邊界的兩個端點所分別對應的X、Y的最大產出,都會增加,因此,整條邊界線將向外移動,但生產邊界外移的方向性則取決於要素...
(黎曼映射定理)若 為單連通區域,其邊界多於一點,為 中任意一點,則在上存在唯一的一個一個把意義對應地映射成單位圓內部的共形映射 ,且 。設 為開圓盤, 為單連通開子集。若 ,則存在一對一的全純映射 ,使 亦全純。換...
考慮依賴於空間變數X的波動方程,分析其在Sturm-Liouville邊界條件下對應性質,研究其Hamilton系統的結構,給出KAM定理,從而在高維空間中得到其擬周期解的存在性與穩定性。波方程描述了自然界各種各樣的波動現象,一直受到國內外眾多學者的...
在函式論方面 ,研究函式值分布論,簡化了在單位圓上單連通域的保形變換的主要定理,給出了邊界對應的理論。在測度論方面,進行了公理化研究,所提出的測度擴張方法被大學教科書普遍採用。此外,對熱力學公理化和狹義相對論也有貢獻。應...
1. 黎曼存在定理 2. 邊界對應定理 第七章習題 第八章 解析延拓 §1. 解析延拓的概念與冪級數延拓 1. 解析延拓的概念 2. 解析延拓的冪級數方法 §2. 透弧解析延拓、對稱原理 1. 透弧直接解析延拓 2. 黎曼施瓦茨對稱原理 §3....
二、黎曼邊界對應定理 習題六 第七章 解析延拓簡介 1 解析延拓的概念和方法 一、基本概念 二、冪級數延拓 三、透弧延拓 2 完全解析函式及單值性定理 一、完全解析函式 二、單值性定理 參考文獻 名詞索引 習題答案與提示 ...
( 1)當 R= 2時 ,由說明 1,這兩個區域可想像為 以赤道為邊界的兩個半球面 ,赤道上有兩個“頂點” 將赤道分成兩條“邊界”,即 R= 2,V= 2,E= 2;於是 R+ V- E= 2,歐拉定理成立.。( 2)設 R= m(m≥ 2)時...
亞純函式的部分分式展式 附錄五 黎曼映射定理及邊界對應定理的證明 1.正規族 2.黎曼映射定理續證 3.邊界對應定理的證明 附錄六 多複變函數 1.解析函式 2.冪級數 3.柯西公式與泰勒展式 習題答案及說明 索引 外國人名譯名對照表 ...
例如,在證明Weierstrass關於級數的定理時,我們利用了全純函式f的任意階導數f(n)在緊集K上的模可以用f在K的鄰域上的模來控制這一事實,使證明得以簡化,而且上述事實在別處還要用到.其他如邊界對應定理和Weierstrass因子分解定理的證明...
冪級數、洛朗級數及孤立奇點相關知識,第五章為留數定理、輻角原理與魯歇定理的相關介紹,第六章教授保形映射中的分式線性變換、施瓦茨-克里斯托費爾變換、黎曼映射定理與邊界對應定理的內容,第七章為調和函式的平均值與極值定理、泊松積分...
12.黎曼定理 38.共形同構和自同構 39.緊性原理 40.黎曼定理 13.邊界對應和對稱原理 41.邊界的對應 42.對稱原理 43.關於橢圓函式的概念 44.模函式和皮卡定理 習題 第五章解析方法 14.整函式與亞純函式的分解 45.米塔-列夫勒定理...
《複變函數》介紹了複變函數的基礎知識,內容包括複數域和複平面上的基本問題,解析函式的一些性質以及初等解析函式,復積分和柯西積分定理,級數理論,留數與輻角原理,許瓦茲原理、開映射原理、最大模原理、黎曼邊界對應原理,共形映射理論...
這個定理將地球形狀和它表面的重力值聯繫起來。Stokes同時解決了這個定理的逆定理:如果已知一個封閉水準面上的重力值,且其外部無質量,就可以確定這個面的形狀。以大地水準面為邊界面的Stokes問題是第一次提出的大地測量邊值問題,並由此...
3單值性定理 3.1沿曲線的解析開拓 3.2單值性定理 習題 第九章共形映射 1共形映射的例子 1.1單連通區域情形 1.2二連通區域情形 2黎曼存在定理 2.1Montel定理 2.2黎曼存在定理 3邊界對應 3.1函式g(w)的連續開拓 3.2函式f(...
