基本介紹
背景
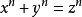
性質
與幾何的聯繫
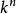
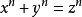
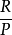
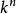
一個環 R中的理想P如果滿足以下條件就稱作素理想:P是R的真理想,且 對任何a,b∈R, 如果乘積ab ∈P,那么a或b中至少有一個屬於P。...
相伴素理想(associated prime ideal)是一種特殊的素理想。包含給定準素理想的最小素理想。準素理想是一種特殊的理想。理想論中理想分解的基礎。素理想是一類特殊...
孤立素理想(isolated prime ideal)是一種特殊的素理想。代數幾何中代數簇的相應概念在環中的引申。素理想是一類特殊理想。它是整數環中素數生成理想的推廣。環是對...
半素理想(semiprime ideal)是與半素環密切相關的概念。環R的理想Q,若對R的任意理想A和某個自然數n,有An⊆Q,就恆有A⊆Q,則稱Q為R的半素理想。它等價...
素理想分解(prime ideal decomposition)亦稱素分解一個域的素理想在擴域中的分解。...... 素理想分解(prime ideal decomposition)[1] 亦稱素分解一個域的素理想在...
理想是集合論中的基本概念之一。理想的概念在現代數學的幾乎每個分支中均有套用,且有許多變體或引申。本原理想(primitive ideal)是與(右)本原環密切相關的一類...
群理想(group ideal )拓撲半群的一類理想.半群S的理想I,若x錢I時,必存在J(x)中一群G,使得G門I=曰,則稱I為群理想.緊緻半群的閉完全素理想是拓撲半素...
素環是一類重要的環。若環R的零理想是素理想,則稱R為素環。整環、單環、本原環都是素環。素環與素理想有如下關係:P是R的素理想若且唯若R/P是素環。....
在數學裡,尤其是在抽象代數裡,交換環的素元(prime element)是指滿足類似整數里的素數或不可約多項式之性質的一個數學物件。須注意的是,素元與不可約元素之間並...
戴德金整環(Dedekind domain)是一維諾特整閉整環。在戴德金整環R中每個準素理想均為素理想的冪,從而每個非零理想均可惟一(不計因子次序)地表示為有限個素理想...
克魯爾維數(Krull dimension)是決定環結構的一個參數,對賦值環的研究有重要意義。設p是R的素理想,R中終止於p的素理想真升鏈p0⊂p1⊂…⊂pn=p的長度n的...
設R是一個交換環,R的理想Q稱為準素理想,如果Q≠R,對任意的a,b∈R,若ab∈Q,a∉Q,則必存在正整數n,使得b∈Q。設I是交換環R的理想,I的根(或稱冪零...
3.dim R=1(其中dim表示克魯爾維數),也即R不是域且非零素理想均為極大理想.在戴德金整環R中每個準素理想均為素理想的冪,從而每個非零理想均可惟一(不計...
準素子模是一類特殊子模,它是準素理想概念的推廣。準素理想是一種特殊的理想。理想論中理想分解的基礎。設Q是交換環R的理想且Q≠R,如果對R中任意元素x,y,xy...
定義 素譜(prime spectrum)在交換環理論與代數幾何中起重要作用的概念.交換環R的全體素理想的集合稱為R的素譜,記為Spec R.其拓撲意義是:若1是R的任意理想,則...
可以證明,K 中全體非零的分式理想在乘法下成一群,而且每個分式理想A 都可以唯一地表成素理想方冪的乘積(公式4)這個群稱為K的理想群,記為IK。...
準素理想的根是一個素理想,這個素理想稱為與Q結合的素理想,或Q是屬於這個素理想的準素理想。交換環R中的理想I稱為有準素分解,如果I=Qi∩…∩Qn,其中Qi,i...
顯然冪零左理想必為詣零左理想,但反之則未必。對R的右理想也有相應的定義。如果P是環R的一個理想, 則P稱為R的一個質理想或素理想。如果環R的零理想{θ}...
分歧指數(ramification index)是在域擴張時,素除子延拓或素理想分解的指數。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴...
由於其定義中帶有“素性”,但又不是素理想,所以周伯壎將primal一詞譯成“素性”。他考慮到,所有理想都是素性理想的整環必有很特殊的性質。誠然,在《關於素性...
《代數數論導引》從現代數學角度儘可能直接地敘述了代數數論的基本內容,由較易的理想論開始,繼而採用了賦值論等方法。包括代數整數環,判別式,諾特環和戴德金環,素...
