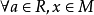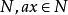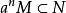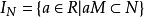準素子模

準素子模是一類特殊子模，它是準素理想概念的推廣。準素理想是一種特殊的理想。理想論中理想分解的基礎。設Q是交換環R的理想且Q≠R，如果對R中任意元素x，y，xy∈Q且x∉Q，恆有正整數n，使得y∈Q，則稱Q是R的準素理想。

基本介紹

• 中文名：準素子模
• 外文名：primary submodule
• 適用範圍：數理科學

簡介

設 R 是一個帶有單位元的交換環，M 是一個 R 模，N 是 M的一個真子模。

如果\意味著存在某個整數 n 使得，那么稱 N 是 M 的準素子模。這時是 R 的一個準素理想。

準素理想

準素理想是一種特殊的理想。理想論中理想分解的基礎。設Q是交換環R的理想且Q≠R，如果對R中任意元素x，y，xy∈Q且x∉Q，恆有正整數n，使得y∈Q，則稱Q是R的準素理想。

素理想是準素理想，但素理想的冪未必是準素理想。

設R是一個環，𝔮是R的一個理想。若由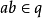但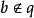必有整數n>0使得，則稱𝔮是R的準素理想。

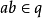
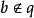
若𝔮是R的準素理想，則r(𝔮)是一個素理想，此時，稱q是r(𝔮)準素的，有時也稱q是屬於r(𝔮)的準素理想。

例如，設p是一個素數，n>0為整數，則(pⁿ)是ℤ的準素理想且。