等周不等式又稱等周定理,說明在周界長度相等的封閉幾何形狀之中,以圓形的面積最大;另一個說法是面積相等的幾何形狀之中,以圓形的周界長度最小。赫爾維茨提出可以將封閉曲線的周界長和曲線所包圍的區域面積之間的關係用不等式表達出來,這個不等式被稱為等周不等式。
基本介紹
- 中文名:等周不等式
- 外文名:Isoperimetric inequality
- 提出者:赫爾維茨
- 學科:數學
- 套用領域:數學、物理
簡介
定義







證明












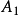























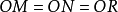





等周不等式又稱等周定理,說明在周界長度相等的封閉幾何形狀之中,以圓形的面積最大;另一個說法是面積相等的幾何形狀之中,以圓形的周界長度最小。赫爾維茨提出可以將封閉曲線的周界長和曲線所包圍的區域面積之間的關係用不等式表達出來,這個不等式被稱為等周不等式。



















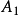























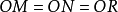




等周不等式又稱等周定理,說明在周界長度相等的封閉幾何形狀之中,以圓形的面積最大;另一個說法是面積相等的幾何形狀之中,以圓形的周界長度最小。赫爾維茨提出可以...
等周定理,又稱等周不等式,是一個幾何中的不等式定理,說明了歐幾里得平面上的封閉圖形的周長以及其面積之間的關係。其中的“等周”指的是周界的長度相等。等周...
著有《數學的發現》、《數學分析中的問題和定理》、《數學物理中的等周不等式》等。 圖書目錄 ~第一卷 譯者的話 序言 對讀者的提示 第一章 歸納方法 第一章...
在20世紀40年代後期,波利亞撰寫了一些有關微分方程的論文以及數學物理方面的一系列論文.其中有些內容,後來出現在與賽格合著的書《數學物理中的等周不等式》(...
現和楊娟娜同學合作的有關等周不等式的論文已被《數學季刊》接受,即將正式發表;目前正指導孫曉偉同學研究一類帶約束條件的等周問題。 [1] ...
美國Lehigh大學訪問教授; 研究方向:整體微分幾何﹑積分幾何﹑凸幾何分析﹑幾何不等式﹑對稱等周不等式,Minkowski isohomothetic不等式等; 在“中國科學”﹑“數學學報...
整體微分幾何部分,系統地介紹了等周不等式、旋轉指標定理、四頂點定理、高斯一波涅公式、卵形面等內容。在附錄中,給出了一些Matlab和Maple程式,用來計算曲線與曲面...
在20世紀40年代後期,波利亞撰寫了一些有關微分方程的論文以及數學物理方面的一系列論文.其中有些內容,後來出現在與賽格合著的書《數學物理中的等周不等式》(Isoperi...
著有《數學的發現》、《數學分析中的問題和定理》、《數學物理中的等周不等式》等。數學與猜想目錄 編輯 ~第一卷譯者的話序言對讀者的提示第一章 歸納方法...
1.4.等周不等式及極高維球面上的函式 2.一些評註 2.1.各種中值 2.2.高維方體與集聚原理 2.3.集聚原理、熱力學、遍歷性 2.4.集聚原理和極限分布 第三章存...
張高勇,1962年出生於重慶潼南,畢業於武漢科技大學,數學家,博士生導師。研究方向是凸幾何分析,幾何與解析不等式、積分幾何等。張高勇教授是世界著名數學家,博士生...
二、等周不等式 三、余面積公式 四、散度定理 五、Talenti比較原理 第七章 Lorentz-Sobolev空間與Orlicz—Sobolev空間 第一節 Lorentz-Sobolev空間。 一、...
獲布達佩斯EotvosLorand大學數學博士學位。著有《數學的發現》、《數學分析中的問題和定理》、《數學物理中的等周不等式》等。數學與猜想第二卷目錄 編輯 ...
1.1等周不等式1.2曲線的旋轉指標1.2.1映射的度數1.2.2旋轉指標定理1.3凸閉曲線2空間曲線的某些整體性質2.1球面上的Crofton公式2.2空間曲線的全曲率...
系統地介紹了2維完備非緊緻黎曼流形上全曲率的幾何,其中包括黎曼幾何預備知識,Cohn Vossen定理,Huber定理,理想邊界,割跡的結構,等周不等式,射線的質量,極點和割跡...
著有《數學的發現》、《數學分析中的問題和定理》、《數學物理中的等周不等式》等。數學的發現:對解題的理解研究和講授目錄 編輯 ...
《傅立葉分析導論》分為3部分:第1部分介紹傅立葉級數的基本理論及其在等周不等式和等分布中的套用;第2部分研究傅立葉變換及其在經典偏微分方程及Radom變換中的...
3.平面曲線的等周不等式 4.空間曲線的全曲率 5.空間曲線的變形 6.Gauss—Bonnet公式 7.Cohn—Vossen和Minkowski的唯一性定理 8.關於極小曲面的Bernstein...
習題4.1.21.3 等周不等式習題4.1.31.4 四頂點定理習題4.1.41.5 等寬曲線習題4.1.51.6 平面曲線上的crofton公式習題4.1.62 空間曲線的整體性質...
《數學物理中的等周不等式》(1951,與賽格合著)[1] [2] 《分析的原理與習題》(1954,與賽格合著)[1] [2] 《數學與猜想》(1954,兩卷。中譯本由科學出版社...
1 變換的概念(1)2 平均值不等式(5)3 三角形的等周不等式(9)4 等周問題的一個套用(16)5 三種顏色的玻璃片(21)6 小孩分糖塊(25)7 糖塊換成砂糖(30)...
而它的“形狀”卻總是相同的,當a=1,}=一1時,凸集S-T用來證明等周不等式.又,若S,T是兩個多胞形,則對任意的.i,閡科夫斯基和集}S+ < 1-})T是一個...
“Bonnesen等周不等式”“準割圓多項式”“n次冪差分的歐拉公式”“算數級數”“三角不等式”“調和級數的一些收斂子級數”等在內,編輯成書,便於讀者進行學習和...
二 平均值不等式 三 三角形的等周不等式 四 等周問題的一個套用 五 三種顏色的玻璃片 六 小孩分糖塊 七 糖塊換成砂糖 八 圓周上的圍棋子 九 最一般的情況...
不僅如此,由此還發現所謂等周不等式不僅對於微分幾何中的某些特殊情形成立,而且對這種同調論有類似的估計,這就使得代數拓撲與測度論聯繫起來了。...
“Bonnesen等周不等式”“準割圓多項式”“n次冪差分的歐拉公式”“算數級數”“三角不等式”“調和級數的一些收斂子級數”等在內,編輯成書,便於讀者進行學習和...
