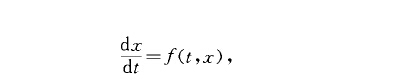

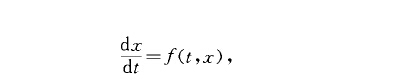

李亞普諾夫函式法(method of I,iapunov func-dons)研究概周期解存在性的一種方法.用李亞普諾夫函式法討論概周期解的存在性問題通常有兩個途徑,或保證緊集KCR”...
李亞普諾夫定理是關於實矩陣特徵值的一個命題,對n階實矩陣A和n階正定矩陣C,若存在正定矩陣B,使得AB+BA′=-C,則A的特徵值的實部必全小於零,這個定理由李亞...
在非線性系統控制當中,為了判定系統穩定性而構建出的函式。通常用V表示。[1] 中文名 李亞普諾夫函式 外文名 Lyapunov Function 用途 用於判定非線性系統的穩定...
李亞普諾夫第二方法就是藉助於一個所謂李亞普諾夫函式V(x,t)及根據微分方程所計算得到的V沿著軌線的導數dV/dt的符號性質來直接推斷穩定性問題。...
李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。克拉索夫斯基於1959年提出了在空間C中解釋軌線的觀點,同時引入李亞普諾夫泛函V(t,φ)的概念...
李亞普諾夫方程,或稱李亞普諾夫矩陣方程,是指對於沒有外部輸入的線性定常連續系統,用以構造李亞普諾夫函式的方程,或使系統原點平衡狀態漸進穩定的充分必要條件。其...
李亞普諾夫函式分解法(decomposition meth-od by I,iapunov function)大系統穩定性分解的一種方法.其一般步驟為: 1.將大系統分解為若干子系統,使得可找出各孤立...
李亞普諾夫第一方法是以級數的形式表示解析方程組的解以研究其穩定性態的方法。...... 李亞普諾夫第一方法是以級數的形式表示解析方程組的解以研究其穩定性態的方...
向量李亞普諾夫函式(vector Liapunov func- tion )由大系統之各個子系統的李亞普諾夫函式構成的向量函式.它可用來判別大系統的穩定性.向量李亞普諾夫函式由美國數學...
隨機李亞普諾夫函式(stochastic I,iapunovfunction)研究隨機動態系統漸近性質的工具.它是幫助人們在不求解隨機微分方程的情況下,定性地研究該隨機系統的漸近性態.例如...
李亞普諾夫指數(Liapunov exponent)簡稱 LE.刻畫動態系統穩定性的重要概念。...... 李亞普諾夫指數(Liapunov exponent)簡稱 LE.刻畫動態系統穩定性的重要概念。...
在自動控制領域中,李雅普諾夫穩定性(英語:Lyapunov stability,或李亞普諾夫穩定性)可用來描述一個動力系統的穩定性。如果此動力系統任何初始條件在平衡態附近的軌跡均...
李亞普諾夫特徵指數(Liapunov characteristicexponent)微分動力系統遍歷論的一個重要概念.在微分動力系統遍歷論的研究中,對流形上微分同胚導出的切空間上的線性變換的...
與此同時,由於對天體力學及天文學中某些問題的研究,需要考慮由微分方程所確定的函式在整體範圍內的性質,法國數學家龐加萊和俄國數學家李亞普諾夫建立了常微分方程...
拉薩爾不變原理是李亞普諾夫第二方法的推廣。這種觀察給出了李亞普諾夫理論的統一認識,且極大地推廣了李亞普諾夫第二方法,現在人們稱這一推廣為拉薩爾不變原理。...
於1892年的博士論文中,開創性地提出求解非線性常微分方程的李亞普諾夫函式法,亦稱直接法,建立了矩陣穩定性的概念及等價表征。這一方法在自動控制、系統問題、微分...
是通過求解系統的微分方程分析運動的穩定性;第二,(直接法)是定性的方法,它不需求解微分方程,而是尋求具有某些性質的函式(稱李亞普諾夫函式),使這些函式與微分方程...
動力系統的運動穩定性的理論,是由俄國數學家李亞普諾夫於19世紀90年代所開創它是研究擾動性因素對運動系統的影響。...
況且他們的研究方法並不相同:林德伯格是基於卷積定理,而李亞普諾夫用的是特徵函式。兩年後林德伯格用自己的方法又獲得更穩定的結果,即所謂的Lindeberg條件。他在機率...
與此同時,由於對天體力學及天文學中某些問題的研究,需要考慮由微分方程所確定的函式在整體範圍內的性質,法國數學家龐加萊和俄國數學家李亞普諾夫建立了常微分方程...
對於黎曼可積函式情形是李亞普諾夫(Ляпунов,А.М.)於1896年證明的。1906年,勒貝格(Lebesgue,H.L.)對於勒貝格平方可積函式給出證明。 [1] ...
一個簡單的存在條件是:“若?為連續有界函式,則邊值問題(1)與(2┡)存在解...方法;50年代以來發展且採用上、下解方法,瓦熱維斯基拓撲方法,李亞普諾夫函式法等...
