李亞普諾夫方程,或稱李亞普諾夫矩陣方程,是指對於沒有外部輸入的線性定常連續系統,用以構造李亞普諾夫函式的方程,或使系統原點平衡狀態漸進穩定的充分必要條件。其形式為見正文。
基本介紹
- 中文名:李亞普諾夫(矩陣)方程
- 外文名:Lyapunov Matrix Equation
- 相關領域:控制理論、自動化
基本概念
李亞普諾夫穩定性
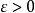
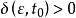


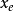
李亞普諾夫第二法
李亞普諾夫方程
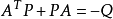
判定和使用方法
穩定性判定
構造函式
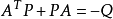

| Refresh | This website www.newton.com.tw/wiki/%E6%9D%8E%E4%BA%9E%E6%99%AE%E8%AB%BE%E5%A4%AB%E6%96%B9%E7%A8%8B is currently offline. Cloudflare's Always Online™ shows a snapshot of this web page from the Internet Archive's Wayback Machine. To check for the live version, click Refresh. |

李亞普諾夫方程,或稱李亞普諾夫矩陣方程,是指對於沒有外部輸入的線性定常連續系統,用以構造李亞普諾夫函式的方程,或使系統原點平衡狀態漸進穩定的充分必要條件。其形式為見正文。


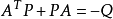
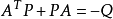

李亞普諾夫方程,或稱李亞普諾夫矩陣方程,是指對於沒有外部輸入的線性定常連續系統,用以構造李亞普諾夫函式的方程,或使系統原點平衡狀態漸進穩定的充分必要條件。其...
李亞普諾夫定理是關於實矩陣特徵值的一個命題,對n階實矩陣A和n階正定矩陣C,若存在正定矩陣B,使得AB+BA′=-C,則A的特徵值的實部必全小於零,這個定理由李亞...
李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。克拉索夫斯基於1959年提出了在空間C中解釋軌線的觀點,同時引入李亞普諾夫泛函V(t,φ)的概念...
在自動控制領域中,李雅普諾夫穩定性(英語:Lyapunov stability,或李亞普諾夫穩定性)可用來描述一個動力系統的穩定性。如果此動力系統任何初始條件在平衡態附近的軌跡均...
李亞普諾夫第一方法是以級數的形式表示解析方程組的解以研究其穩定性態的方法。... 李亞普諾夫第一方法是以級數的形式表示解析方程組的解以研究其穩定性態的方法...
李亞普諾夫函式法(method of I,iapunov func-dons)研究概周期解存在性的一種方法.用李亞普諾夫函式法討論概周期解的存在性問題通常有兩個途徑,或保證緊集KCR”...
李亞普諾夫特徵數是指定量描述變係數線性方程組解的穩定性態的一種數。... 李亞普諾夫特徵數是指定量描述變係數線性方程組解的穩定性態的一種數。...
動力系統的運動穩定性的理論,是由俄國數學家李亞普諾夫於19世紀90年代所開創它是研究擾動性因素對運動系統的影響。...
什麼是運動穩定學?這是一門新興的研究運動狀態控制的學科,運用定性的方法尋求具有某些性質的函式(稱李亞普諾夫函式),使這些函式與微分方程相聯繫的一種學說。...
1 概念 2 曲面積分 3 拉普拉斯方程 4 李亞普諾夫曲面 雙層位勢概念 編輯 雙層位勢是通過基本解的法嚮導數定義的一個曲面積分,也是拉普拉斯方程的一個特解。...
