基本介紹
定義

與線性無關解

線性微分方程
描述






定理的證明




例子



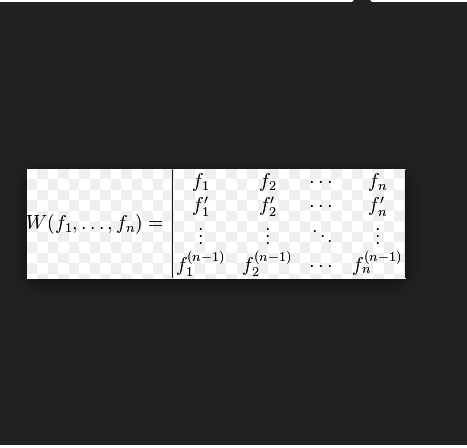















朗斯基行列式準則 朗斯基行列式準則(criterion via Wronski determinant)是1993年經全國科學技術名詞審定委員會審定發布的數學名詞。發布時間 1993年經全國科學技術名詞審定委員會審定發布的數學名詞。出處 《數學名詞》
具體來說,是把動力回響展開某參數的級數,並用朗斯基行列式證明其線性無關性,並用級數比較法證明了其收斂性,因而是一個完備的解。這是本項目研究的一大進展。用此疊代法可以求出有限體積非均勻介質的自由振動頻率及其振型,採用模態...
基本解組是指能用線性組合構造出齊次線性微分方程全部解的線性無關的解系。微分方程基本解組的存在性是由微分方程的基本理論保證的,而方程的 n 個解的線性無關性則可以通過朗斯基行列式準則加以判定。簡介 n 階齊次線性微分方程組 考慮...
方程內容 非線性偏微分方程 其中 函式子解 利用sech函式展開法可得卡東穆塞夫-彼得韋亞斯維利方程的sech函式解和tanh函式解。函式解 通過朗斯基行列式展開法可得卡東塞穆夫-彼得韋亞斯維利方程多個雅可比橢圓函式解 ...
直接法微擾理論在套用範圍和與通常微擾理論的聯繫上遠好於以反散射為基礎的微擾理論,自Kaup求得線性化方程之基本解後,求基本解的正交性和證明完備性的辦法五花八門.我們在著手建立DNLS方程的直接法微擾理論時,注意到通常從朗斯基行列式...
本書在講述非線性薛丁格方程的各類物理背景的基礎上, 對其基本解, 特別是有理形式表示的畸形波解的求解方法進行了闡述, 包括直接方法、雙線性方法、達布變換法和朗斯基行列式方法等, 分別重點給出在流體力學、非線性光學、電漿物理、...
第6章行列式362 6.1簡介363 6.2行列式的代數餘子式展開363 6.3初等變換與行列式368 6.4克萊姆法則376 6.5行列式的套用:逆矩陣與朗斯基 行列式381 第7章特徵值及其套用391 7.1二次型392 7.2微分方程組400 7.3化海森伯格型407...
