解空間是指齊次線性方程組所有解的集合構成一個向量空間,也就是一個集合。
基本介紹
- 中文名:解空間
- 外文名:solution space
- 實質:數學術語
- 組成:由解向量組成
- 性質:一個集合
定義
基礎解系
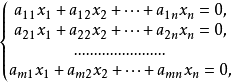

解空間是指齊次線性方程組所有解的集合構成一個向量空間,也就是一個集合。
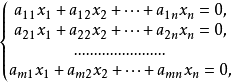

解空間是指齊次線性方程組所有解的集合構成一個向量空間,也就是一個集合。...... 解空間是指齊次線性方程組所有解的集合構成一個向量空間,也就是一個集合。...
《理解空間》是2008年5月中央編譯出版社出版的圖書,作者是馮雷。本書主要講述了 20世紀初繪畫空間的變異以及 20世紀初繪畫空間的意義。...
理解空間:20世紀空間觀念的激變是一部其他類型網路小說,作者是馮雷。...... 本書圍繞著如何理解現代空間觀念變化這一主題展開,闡述了20世紀初繪畫空間的變異、心理...
《空間認知能力的測驗研究》是楊孟萍,石德澄撰寫的一篇論文。...... 一般認為智力包括語言因素,散量因素和非語言性因素,其中非語言性因素就是指的空間能力因素。運...
解向量是線性方程組的一個解。因為一組解在空間幾何里可以表示為一個向量,所以叫做解向量。解向量在矩陣和線性方程組中是常用概念。如果n元齊次線性方程組Ax=0的...
該算法在具體執行時,把全部可行的解空間不斷分割為越來越小的子集(稱為分支),並為每個子集內的解的值計算一個下界或上界(稱為定界)。在每次分支後,對凡是...
分支限界法常以廣度優先或以最小耗費(最大效益)優先的方式搜尋問題的解空間樹。在分支限界法中,每一個活結點只有一次機會成為擴展結點。活結點一旦成為擴展結點,就...
當 n=3 時,其解空間是{ (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, ...
搜尋算法是利用計算機的高性能來有目的的窮舉一個問題解空間的部分或所有的可能情況,從而求出問題的解的一種方法。現階段一般有枚舉算法、深度優先搜尋、廣度優先...
子集樹是一個數學學科辭彙,屬於函式類,當所給問題是從n個元素的集合S中找出S滿足某種性質的子集時,相應的解空間稱為子集樹。...
[7] 在下面分析回溯法和分支限界法時都直接或間接用到解空間樹。在解空間樹中的每一個結點確定所求問題的一個問題狀態(problem state)。由根結點到其它結點的所...
子集樹:當所給的問題是從n個元素的集合S中找出滿足某種性質的子集時 相應的解空間樹稱為子集樹 子集樹通常有2 子集時,相應的解空間樹稱為子集樹。子集樹...
與貪婪算法一樣,這種方法也是用來為組合最佳化問題設計求解算法的,所不同的是它在問題的整個可能解空間搜尋,所設計出來的算法雖其時間複雜度比貪婪算法高,但它的...
考試內容:線性方程組的克萊姆(Cramer)法則齊次線性方程組有非零解的充分必要條件非齊次線性方程組有解的充分必要條件解空間 非齊次線性方程組的通解...
黑板系統是一種問題求解模型,是組織推理的步驟、控制狀態數據和問題求解之領域知識的概念框架,它將問題的解空間組織成一個或多個套用相關的分級結構。分級結構的每...
在三維空間中,最常見的另類坐標系統是圓柱坐標系和球坐標系。平面解析幾何曲線方程 在解析幾何當中,任何方程都包含確定面的子集,即方程的解集。例如,方程y=x在...
模擬退火算法(Simulate Anneal,SA)是一種通用機率演算法,用來在一個大的搜尋空間內找尋命題的最優解。模擬退火是由S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在...
