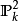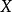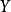基本介紹
- 中文名:有理映射
- 外文名:rational mapping
- 套用學科:代數幾何
- 相關術語:雙有理等價
- 定義:在概形的稠密開集上的態射
- 套用領域:數學 幾何學
定義,定義延伸,例子,擴展,
定義
固定概形 。考慮所有的資料
。考慮所有的資料 ,其中
,其中 是稠密開集,而
是稠密開集,而 是態射;這些資料代表了
是態射;這些資料代表了 上“部分定義”的態射,
上“部分定義”的態射, 代表
代表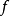 的定義域。定義下述等價關係:
的定義域。定義下述等價關係:






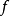

此外,注意到稠密性保證 也是
也是 中的稠密開集。當
中的稠密開集。當 不可約,則所有非空開集都是稠密的。若再假設
不可約,則所有非空開集都是稠密的。若再假設 既約而
既約而 是分離概形,則任一等價類有唯一一個定義域最大的代表元。
是分離概形,則任一等價類有唯一一個定義域最大的代表元。





若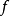 是從
是從 到
到 ,而
,而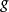 是從
是從 到
到 的有理映射,則一般並不能定義其合成
的有理映射,則一般並不能定義其合成 。但是當
。但是當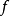 的像(對某個,因而對每個代表元
的像(對某個,因而對每個代表元 )在
)在 中稠密時,對每個
中稠密時,對每個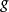 的代表元
的代表元 ,
, 皆非空,此時可以定義
皆非空,此時可以定義 。
。
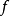


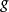



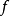


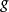



定義延伸
有理映射是代數幾何中常見的對象。
換句話說,有理映射幾乎處處有定義,那些沒定義的點全體只占有很小的維數。
在高維代數幾何中, 人們也在試圖尋找高維代數簇在雙有理等價意義下的極小模型,這一研究分支稱為雙有理幾何。
例子
其中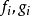 是多項式。該有理映射可以在
是多項式。該有理映射可以在 上定義。
上定義。
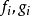

擴展
優勢映射與雙有理等價
之前考慮合成問題時,曾利用像的稠密性條件;滿足該條件的有理映射稱為優勢映射。由於優勢映射可以作合成,定義從概形 到
到 的雙有理等價為一個優勢映射
的雙有理等價為一個優勢映射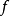 ,使得存在另一個從
,使得存在另一個從 到
到 的優勢映射
的優勢映射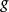 ,使
,使 、
、 。
。


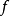


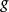




雙有理等價的例子
雙有理等價的定義較同構寬,因為我們容許態射在某維度較低的閉集上未定義。一個例子是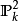 與
與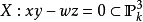 ,兩者雙有理等價,而並不同構。原因如下:
,兩者雙有理等價,而並不同構。原因如下: 中的任兩條閉曲線都有交點,而在
中的任兩條閉曲線都有交點,而在 }中,
}中, 與
與  不相交,因而
不相交,因而 與
與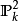 並不同構。
並不同構。
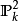
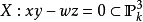





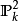
另一方面, 的函式域可以在仿射開集
的函式域可以在仿射開集 上計算,此開集的座標環是
上計算,此開集的座標環是 ,其函式域是
,其函式域是 ;這也是
;這也是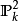 的函式域,於是二者雙有理等價。若細審上述論證,事實上能寫出所求雙有理等價的式子。
的函式域,於是二者雙有理等價。若細審上述論證,事實上能寫出所求雙有理等價的式子。