基本介紹
- 中文名:線性系
- 外文名:linear system/linear series
- 適用範圍:數理科學
簡介








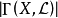
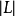

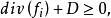
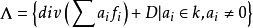


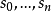
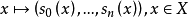


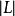
固定分支
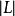
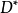

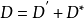
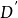
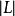
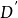

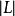



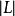

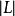









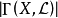
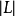

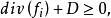
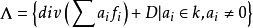


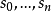
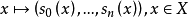


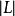
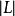
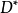

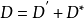
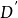
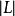
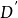

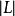



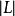

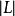
線性系是代數幾何中最基礎的研究對象之一。線性系是代數簇上的一族線性等價的有效除子,它為射影空間所參數化。...
線性系統理論中用幾何學的語言和方法研究線性系統的一個理論分支。...... 線性系統幾何理論產生於70年代初期,以W.M.旺納姆為代表的研究者已形成為線性系統理論研究...
抽象線性系統(abstract linear system)是線性系統概念的一種推廣。線性系統的系統過程滿足疊加原理時的一種模式。在這類系統中,當系統無控制作用時,其過程的和及...
介紹 正線性系統(positive linear system)一類形如線性的動態系統.其狀態變數始終只能取正實數值.這種狀態空間受限的系統,常用於描述系統包含物理上不可能為負的狀態...
線性系統代數理論是以狀態空間法為主要工具研究多變數線性系統的理論。20世紀50年代以後,隨著航天等技術發展和控制理論套用範圍的擴大,經典線性控制理論的局限性日趨...
《線性系統與信號》是2006年西安交通大學出版社出版的一本書籍,作者是美國的B.P.拉茲。該書全面系統地論述了線性系統與信號分析的基本理論和方法。...
線性系統模型:inear system mode{系統模型的一種,其變數之間的關係是線性的。而時間變數是離散的系統模型,則為離散時間線性系統模型( discrete-time linear system...
線性系統是一數學模型,是指用線性運運算元組成的系統。相較於非線性系統,線性系統的特性比較簡單。線性系統需滿足線性的特性,若線性系統還滿足非時變性(即系統的輸入...
空間不變線性系統是指任一系統有一輸入,就有一輸出,也可以講系統將輸入函式變換成輸出函式。如一照相機,有一物(輸入)就相應產生一個像(輸出),照相機的作用是...
《線性系統控制理論》是2000年華東師範大學出版社出版的圖書,作者是陳樹中。該書闡述的是21世紀80年代之前線性理論研究方面的主要結論,內容通俗易懂,讓對線性控制...
準線性系統(quasi linear system)是指在實際問題中所建立的非線性系統模型應該能夠在一定的條件下線性化使得解決問題的方法簡單化而不致超過允許誤差的系統模型。對於...
《線性系統》簡要介紹了線性系統的基本理論和基本結構性質,為讀者學習新近發表的與線性系統理論及其套用有關的大量文獻提供一個堅實的理論基礎。全書共分為9章,內容...
切換線性系統(switch linear system)一類混雜系統.它由若干線性系統模型依一定條件和規則,在相空間中相互切換演化過程而構成的動態系統. 這類系統本質上是非線性的,...
《線性系統與信號(第2版)》是2006年西安交通大學出版社出版的圖書,作者是拉茲(美)。該書全面系統地論述了線性系統與信號分析的基本理論和方法。...
最小相位線性系統(minimum phase linear sys-tem)一類特殊的線性控制系統.用}(C,A,B)表示線性控制系統 那么稱}(C,A,B)為最小相位線性系統. ...
5。 Bombieri:如果n≧5, 那么由多重典範線性系|nK_X|誘導的多重典範映射Φ_n是同構的。 有許多數學家對此作出了重要貢獻, 比如崛川寅二(Horikawa), 肖剛,Be...
