在空間中,滿足n次代數方程f(x,y,z)=0的點P(x,y,z)的全體,稱為n次代數曲面。還可把這個概念推廣到高維的情況。
基本介紹
- 中文名:代數曲面
- 外文名:algebraic surface
- 所屬學科:數學
- 舉例:等橢球面、雙葉雙曲面等
- 別稱:n次代數曲面、n次曲面
發展歷程

定義



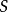

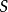


代數曲面的齊次方程式

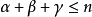

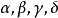
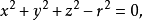

曲面的確定條件數

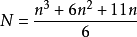
代數曲面的階


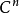
 圖1(a)
圖1(a) 圖1(b)
圖1(b) 圖1(c)
圖1(c)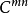

在空間中,滿足n次代數方程f(x,y,z)=0的點P(x,y,z)的全體,稱為n次代數曲面。還可把這個概念推廣到高維的情況。




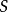

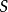



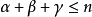

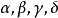
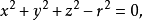


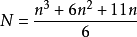


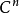
 圖1(a)
圖1(a) 圖1(b)
圖1(b) 圖1(c)
圖1(c)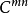
在空間中,滿足n次代數方程f(x,y,z)=0的點P(x,y,z)的全體,稱為n次代數曲面。還可把這個概念推廣到高維的情況。...
代數幾何,是現代數學的一個重要分支學科。它的基本研究對象是在任意維數的(仿射或射影)空間中,由若干個代數方程的公共零點所構成的集合的幾何特性。這樣的集合通常...
《代數曲面和全純向量叢》是2009年6月1日世界圖書出版公司出版的圖書,作者是(美國)弗里德曼(Friedman.R.)。...
代數幾何法是現代數學的重要研究方法之一。任意維數空間中,由若干代數方程的公共零點構成的集合,稱為代數簇。研究代數簇的兒何特性的方法稱為代數幾何法。代數幾何...
代數幾何研究就是平面解析幾何與三維空間解析幾何的推廣。大致說來,它是研究n維仿射空間或n維射影空間中多項式方程組的零點集合構成的幾何對象之特性及其上的三大結構...
設X是射影代數曲面, 如果X不包含(-1)-曲線, 並且它的第一陳類c_1(X) 以及結構層 O_X 的上同調 示性類χ(O_X),分別滿足:c_1^2(X)>0, χ(O_...
代數曲面的纖維化基本信息 編輯 作者:肖剛 出版社:上海科學技術出版社 出版年:1992.01 頁數:180 定價:5.45 裝幀:19cm 叢書:現代數學叢書 ISBN:9787532325399[1]...
K3曲面是一類重要的緊復曲面,在此“曲面”系指復二維,視作實流形則為四維。...... 在數學領域的代數幾何及複流形理論中,K3曲面是一類重要的緊復曲面,在此“...
《國外數學名著系列34:代數幾何2代數簇的上同調,代數曲面》由兩部分構成,前半部分著重介紹代數簇的上同調,後半部分討論代數曲面。本書還包含涉及不同主題的大量...
《代數曲面拼接的理論與算法研究》是2011年科學出版社有限責任公司出版的圖書,作者是厲玉蓉。...
曲面纖維化是代數幾何中的重要課題。...... 設S是光滑代數曲面,C是光滑代數曲線.如果存在一個全純的滿態射 f:S→C,那么就稱S有一個到的C纖維化。...
恩內佩爾曲面(Enneper's surface)一種重要的極小曲面.在外爾斯特拉斯公式中,令f.=2,}=}=u+iv,D=R,得 該曲面稱為恩內佩爾曲面.它是代數曲面,其高斯映射是...
《代數幾何Ⅱ》是2007年1月科學出版社出版的圖書,作者是沙法列維奇。...... 《國外數學名著系列34:代數幾何2代數簇的上同調,代數曲面》由兩部分構成,前半部分著重...
