基本介紹
- 中文名:仿射坐標系
- 外文名:affine coordinate system
- 特點:點的坐標與原點的選取有關
- 相關:仿射標架
- 一級學科:數學
- 二級學科:仿射幾何學
坐標系
仿射坐標系





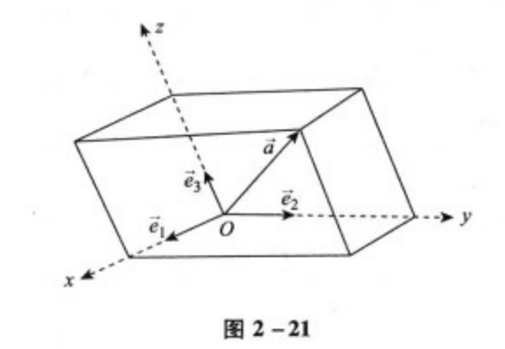 圖1
圖1定義


 圖2
圖2




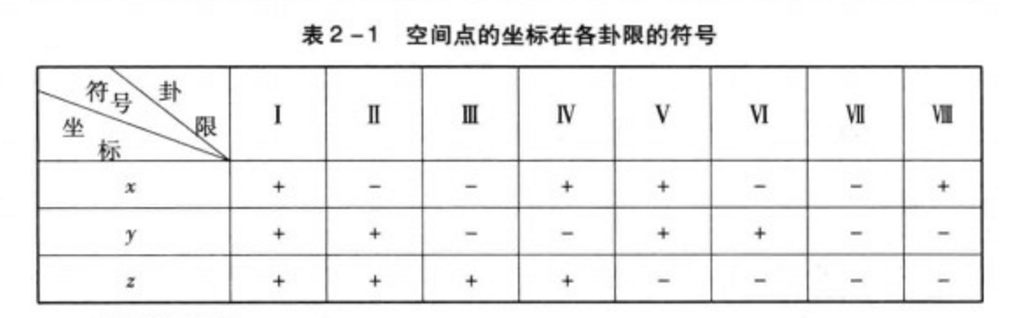 表1
表1向量的坐標







向量坐標運算













 圖1
圖1

 圖2
圖2




 表1
表1













仿射坐標系(affine coordinate system)是解析幾何中仿射坐標系的推廣。設V是實n維線性空間,A是關於V的仿射空間,A中一個固定點O與V的一個基(e1,e2,e3)稱為A...
仿射坐標變換公式(transformation formula foraffine coordinates)仿射坐標系改變時坐標的變換公式。...
平面仿射坐標變換是一種坐標變換,指平面上任一點對於兩個仿射坐標系的坐標之間的對應關係。平面上點的仿射坐標變換公式和平面上向量的仿射坐標變換公式。...
中心仿射變換是指含一個不變點的仿射變換,這個不變點稱為中心仿射變換的中心。在以變換中心為坐標原點的仿射坐標系中,中心仿射變換公式右端的常數項為0。例如,在...
仿射空間中最重要的變換是仿射變換,它的特徵是將共線的三點變為共線的三點。給定仿射坐標系後,仿射變換有明確的代數表示。仿射變換全體構成的變換群稱為仿射變換...
坐標系統是描述物質存在的空間位置(坐標)的參照系,通過定義特定基準及其參數形式來實現。坐標是描述位置的一組數值。按坐標的維度一般分為一維坐標(公路里程碑)和...
如果將平面P仿射變換到平面P',則取笛卡爾坐標系XOY,並變換為X'O'Y',U點相M點變換為對應點U’和M‘。在新坐標系里取U‘力單位點,其度量單位在O’X'軸上...
射影坐標是在射影幾何學中和在研究圖形的純射影性質時,常採用的一種坐標系。它在射影幾何中的作用,就象直角坐標系在歐氏幾何中和仿射坐標系在仿射幾何學中的作用...
直線系(system of straight lines)亦稱直線束,是具有某一共同性質的直線的集合。如在平面仿射坐標系中,與已知直線Ax+By+C=0平行的所有直線組成一個直線系,它的...
《幾何學概論》分為三個部分,其中第一部分使學生了解幾何學發展簡史和非歐幾何的幾種經典模型;第二部分主要講解歐氏幾何與二次曲線的度量性質及分類,仿射坐標系、...
標架一般是完全決定空間坐標系來用的,所以空間坐標系也可以用標架 {O;e1,e2,e3} 來表示,這時候點 O 就可以叫做坐標原點,而向量 e1,e2,e3 都叫做坐標向量...
右手系(right-hand system)是在空間中規定直角坐標系的方法之一。此坐標系中x軸,y軸和z軸的正方向是如下規定的:把右手放在原點的位置,使大姆指,食指和中指互...
平面劃分空間(cutting space by plane).在空間仿射坐標系中,一個平面方程為 [1] :將以空間任意不在平面二上的兩點 和 為端點的線段 分成比為 的兩段.當 與...
在平面仿射坐標系中,圓錐曲線的方程都是二元二次方程,因此,圓錐曲線又稱為二次曲線。而且平面與任何二次曲面的交線總是二次曲線。例如,圓柱的斜截口即為橢圓。...
3 6平面與直線在仿射坐標系下的方程91 3 7例題97 第4章矩陣的秩與相抵分類103 4 1向量組的線性相關性103 4 2向量組的秩107 4 3矩陣的秩110 4 4平面之間...
在平面仿射坐標系中,一直線l:Ax+By+C=0將此平面內l以外的任意兩點P1(x1,y1)和P2(x2,y2)為端點的線段P1P2所分成的比為當Ax1+By1+C與Ax2+By2+C異...
