基本介紹
- 中文名:直線劃分平面
- 所屬學科:數學
- 所屬問題:平面解析幾何
- 簡介:直線坐標平面為兩個半平面
基本介紹

相關性質及其證明



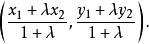



















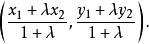














直線劃分平面是解析幾何研究的重要問題之一。任一直線l:Ax+By+C=0把平面內的點分成三個點的集合:(1)直線上的點的集合,點到直線的距離δ=0;(2)不包含原點...
直線分平面公式是指n條直線最多能把平面分成1+1+2+3+……+n個部分。...... 如果沒有一條直線,那么平面就可以看作1個部分;如果有1條直線,那么平面就被分成...
一 如果一個平面內有兩條相交直線都平行於另一個平面,那么這兩個平面平行。...直線切割平面是指用直線將平面劃分成多個部分。n條直線最多將平面分割成1+ 個...
直線形(rectilinear figure)是一類簡單的幾何圖形,指由直線、射線、線段組成的圖形,直線形常把它所劃分的內部區域包括在內。...
它有無數條對稱軸,其中一條是它本身,還有所有與它垂直的直線(有無數條)對稱軸。在平面上過不重合的兩點有且只有一條直線,即不重合兩點確定一條直線。在球面上...
或曰:線面所成角,直線與平面所成角 1、定義: 當直線與平面垂直時,規定這條直線與該平面成直角。 當直線與平面平行或在平面內時,規定這條直線與該平面成0°...
平行平面截直線定理,是指兩條直線穿過一組平行平面,則其各平面的交點所組成的線段成比例的一個立體幾何定理。...
第一章 直線劃分平面問題 知識掃描 範例精析 佳題賞析 能力訓練 第二章 簡單的線性規劃 知識掃描 範例精析 佳題賞析 能力訓練 第三章 動態線性規劃 知識掃描 ...
直線與平面斜交(oblique intersection betweena line and a plane)空間直線和平面的一種位置關係一條直線和一個平面相交,但不和這個平面垂直,則這條直線稱為這個...
斜率,亦稱“角係數”,表示一條直線相對於橫軸的傾斜程度。一條直線與某平面直角坐標系橫軸正半軸方向的夾角的正切值即該直線相對於該坐標系的斜率。 如果直線與x...
二分法必然符合劃分的規則。劃分數學方面 編輯 在數學上,有一類問題,都是研究劃分空間而成空間區域的。比如,平面上有n條直線,它把平面劃分成幾個區域呢?這個問題...
《超級數學專題題典:直線和平面》是2007年世界圖書出版公司出版的圖書。...... 《超級數學專題題典:直線和平面》是2007年世界圖書出版公司出版的圖書。...
平面跡線(trace line of plane)平面上的特殊直線.平面與投影面的交線稱為平面跡線.如圖1,圖2所示.平面與V面的交線稱為正面跡線,與H面的交線稱為水平跡線...
本書以專題的形式對高中數學中直線與平面的重點、難點進行了歸納、總結,全書共分兩大部分,即解題方法編和試題精粹編,內容豐富,涵蓋面廣,可使學生深入理解直線與...
3 桿件、橫截面與軸線 4 軸線的劃分原則 5 軸線常用專業名詞 軸線...若軸線始終與該平面圖形垂直,是為正桿,否則為偏桿。若軸線為直線,是為直桿,...
