平面內的一條直線把這個平面分成兩部分,每一部分對這個平面來說,都叫做半平面。包括這條直線的半平面叫做閉半平面,否則叫做開半平面。
基本介紹
- 中文名:半平面
- 外文名:half plane
- 所屬學科:數學
- 分類:開、閉半平面,左、右半平面等
定義
定義1
定義2






定義3
定義4


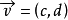
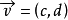

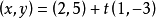
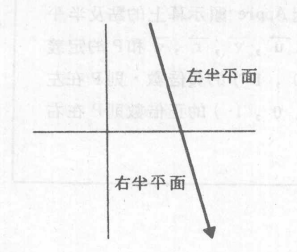 圖1
圖1 圖2
圖2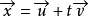

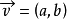



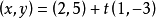



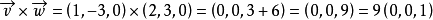
 圖3
圖3

複平面的半平面

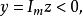

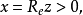
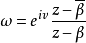

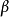
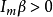

平面內的一條直線把這個平面分成兩部分,每一部分對這個平面來說,都叫做半平面。包括這條直線的半平面叫做閉半平面,否則叫做開半平面。








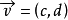
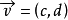

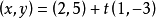
 圖1
圖1 圖2
圖2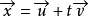

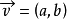



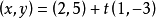



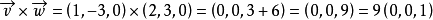
 圖3
圖3


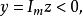

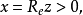
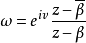

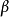
平面內的一條直線把這個平面分成兩部分,每一部分對這個平面來說,都叫做半平面。包括這條直線的半平面叫做閉半平面,否則叫做開半平面。...
平面角由射線——點——射線構成,是從平面內一點出發的兩條射線(半直線)所組成的圖形。平面角的大小定義為以兩射線交點為圓心的圓被射線所截的弧長與半徑之比,...
直線劃分平面是解析幾何研究的重要問題之一。任一直線l:Ax+By+C=0把平面內的點分成三個點的集合:(1)直線上的點的集合,點到直線的距離δ=0;(2)不包含原點...
龐加萊複數平面模型(Poincaré complex plane model)是解釋羅氏平面幾何的模型。這個模型是龐加萊((J.-)H.Poincaré)首先提出來的,因為該模型的點是在複數上半...
施瓦茲對稱原理是把解析函式定義域作對稱擴大的解析開拓法,其基本原理是:設ƒ的定義域G在上半平面內,且以實軸上線段у為部分邊界,ƒ在G+γ上有定義且連續,...
從一條直線出發的兩個半平面所組成的圖形叫做二面角,這條直線叫做二面角的棱,這兩個半平面叫做二面角的面。...
系統穩定是指系統的全部閉環特徵根均在s平面的左半平面,這等價於若系統穩定則在右半平面上沒有任何閉環特徵根。...
模形式論是數學上一個滿足一些泛函方程與增長條件、在上半平面上的(復)解析函式。因此,模形式論屬於數論的範疇。模形式也出現在其他領域,例如代數拓撲和弦理論。...
斜二面角(oblique dihedral angle)是一類二面角的統稱,即銳二面角與鈍二面角的統稱。有公共邊緣的兩個半平面所組成的圖形稱為二面角,也叫二面形,這公共邊緣稱為...
若存在狀態反饋矩陣K使得A+BK的特徵值全在左半平面,稱線性定常系統(A,B,C,D)是能穩的。顯然,若(A,B)能控,則存在狀態反饋矩陣K,使得A+BK的特徵值任意配...
對於連續時間系統,如果控制系統開環傳遞函式的所有極點和零點均位於s左半平面上,則稱該系統為最小相位系統。對於離散時間系統,則是所有零極點均位於單位圓內。 一...
在微分幾何中,曲率的倒數就是曲率半徑,即R=1/K。平面曲線的曲率就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。對於...
平面角是直角的二面角叫直二面角 平面內的一條直線把平面分為兩部分,其中的每一部分都叫做半平面,從一條直線出發的兩個半平面所組成的圖形,叫做二面角(這條直線...
由於對於一個穩定的閉環系統來說,其在S右半平面肯定是無特徵根,即Z=0,因此,Nyquist穩定判據就可以這樣認為,若Nyquist曲線包圈(-1,j0)點的圈數等於開環傳函在...
具有公共棱的兩個二面角,如果它們的兩個面重合,另兩個面組成一個平面,就說它們互為鄰補二面角supplementary adjacent dihedral angle )。...
模函式,屬解析函式論學科,是上半複平面上屬於亞純函式的一類,模形式是模函式的推廣。定義在單位圓(或上半平面)內部且以其周界為自然邊界的某種特殊解析函式。...
《固體接觸力學》是中國鐵道出版社出版的圖書,本書主要介紹在平面和空間情況下的無摩擦接觸理論、摩擦接觸理論、材料非線性接觸理論等。對於了解接觸問題的數學模型的...
θ為常數時 半平面 一 柱面坐標系設M(x,y,z)為空間內一點,並設點M在xoy面上的投影P的極坐標為r,θ,則這樣的三個數r, θ,z就叫點M的柱面坐標。規定...
施瓦茨·克里斯托費爾映射,定義為考慮複平面上一個多邊形,把上半平面共形地映射到一個多邊。...
ρ擬對稱函式完全刻畫了上半平面的擬共形映射,容易看出,任何一個上半平面的擬共形映射在實軸上的限制滿足ρ擬對稱性。...
時趨於零,因此圍道積分應在下半平面進行;反之式(3.61)第二項圍道積分應在上半平面進行,於是根據留數定理 (3.62)對上式求傅立葉反變換,得時域無限均勻媒質下...
§1 集中力作用在彈性半空間內1.1 Lorentz問題1.2 Mindlin問題1.3 混合問題A1.4 混合問題B§2 集中力作用在彈性半平面內§3 從空間問題的解導出平面問題的解...
