具有公共棱的兩個二面角,如果它們的兩個面重合,另兩個面組成一個平面,就說它們互為鄰補二面角supplementary adjacent dihedral angle )。
基本介紹
- 中文名:鄰補二面角
- 外文名:supplementary adjacent dihedral angle
- 所屬學科:數學
- 所屬問題:立體幾何(空間角)
- 簡介:既相鄰又互補的兩個二面角
定義,相關概念,例題解析,
定義
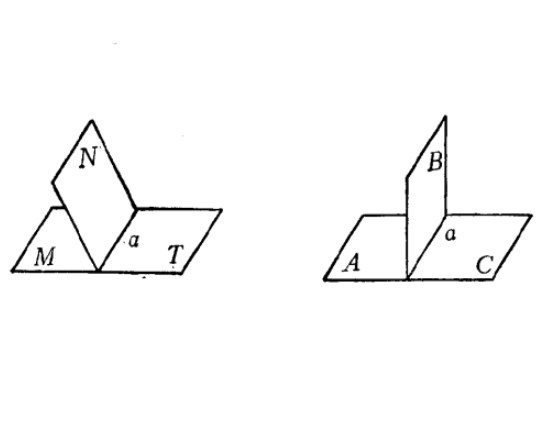
鄰補二面角是指兩個位置相關的二面角,既相鄰又互補的兩個二面角稱為鄰補二面角。如圖1中的MaN和NaT。如果兩個鄰補二面角相等,則這兩個二面角中的每一個都叫做直二面角。兩個鄰補二面角的平分面互相垂直。
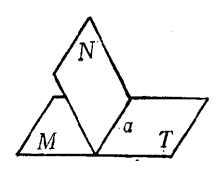 圖1
圖1相關概念
一個平面內的一條直線把這個平面分成兩個部分,每一部分都叫做半平面,從一條直線出發的兩個半平面所組成的圖形叫做二面角,這條直線叫做二面角的棱,這兩個半平面叫做二面角的面,如在圖2中,從直線AB出發的兩個半平面M、N就組成了一個二面角,AB是它的棱,M、N是它的面。
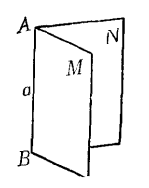 圖2
圖2二面角的表示法通常是把表示棱的字母寫在中間,表示面的字母寫在兩旁,中間用兩條短橫線隔開(如果棱用小寫字母表示時可以不必用橫線隔開),如圖2中的二面角可記作:二面角M-AB-N或二面角MaN。
二面角也可以看作是從一條直線出發的一個半平面繞著這條直線旋轉,它的起始位置和終止位置所組成的圖形。這個二面角的大小可由這個半平面旋轉量的大小來確定。
二面角和平面幾何里的角是很類似的。如果把平面幾何的角的頂點換成二面角的棱,角的兩邊換成二面角的面,那么就很容易理解下述二面角的有關概念:
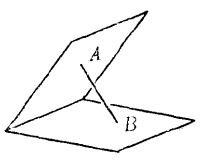 圖3
圖3(1) 在二面角兩面上各任取一點, 如圖3中的A和B,那么線段AB上的點叫做這二面角的內點,一切內點構成二面角的內部。
(2) 如果兩個二面角重疊起來完全重合,這兩個二面角叫做相等的二面角。
(3) 如果兩個二面角有公共的棱和一個公共面, 並且它們的另一個面分別在這公共面的異側,這兩個二面角叫做互為鄰二面角,如圖4中的PaQ和QaR,二面角PaR叫做PaQ與QaR的和,二面角PaQ叫做PaR與QaR的差,QaR也是PaR與PaQ的差。這時,我們就說二面角PaR大於PaQ (或QaR),或者說PaQ(或QaR)小於PaR。
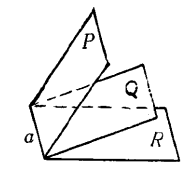 圖4
圖4(4) 如果兩個鄰二面角,其它兩個面在同一平面內,這樣的兩個二面角叫做互為鄰補二面角,如圖1中的MaN和NaT,這時二面角MaT叫做平二面角,如果兩個鄰補二面角彼此相等,其中每一個二面角叫做直二面角,如圖5中的AaB和BaC。
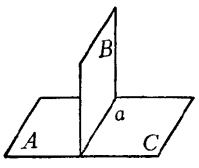 圖5
圖5例題解析
【例1】在長方體ABCD-A1B1C1D1中,BC=BB1=1/2AB=a,E是棱AB的中點,連結D1E、D1A、D1C,求二面角A-D1E-C的大小。
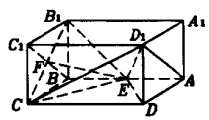 圖5
圖5分析 如圖5。由於二面角A-D1E-C是一個鈍角,需要把面AD1E延展,先求出它的鄰補二面角(銳角)C1-D1E-C的大小,再求出原二面角的大小。
解如圖5,連B1E、BC1、B1C,設BC1∩B1C=F,再連EF。
BC1//D1A A、D1、E、F共面
A、D1、E、F共面


在矩形ABCD中,因為AE=EB= BC,
所以DE⊥ EC,
又 D1D⊥平面ABC,所以D1E⊥EC
同理,D1E⊥EB1
從而 D1E⊥平面B1EC,所以D1E⊥EF,
於是,∠CEF就是二面角C1-D1E-C的平面角,
所以EB⊥平面BCB1,BF⊥B1C,
所以EF⊥FC,
在Rt△EFC中,

所以

故 二面角A-D1E-C的大小為180°- 30°,即150°。
解說 由本例知,若所求二面角的大小較難計算時,我們可先求出它的鄰補二面角的大小θ,則180°- θ(或π- θ)即為所求。