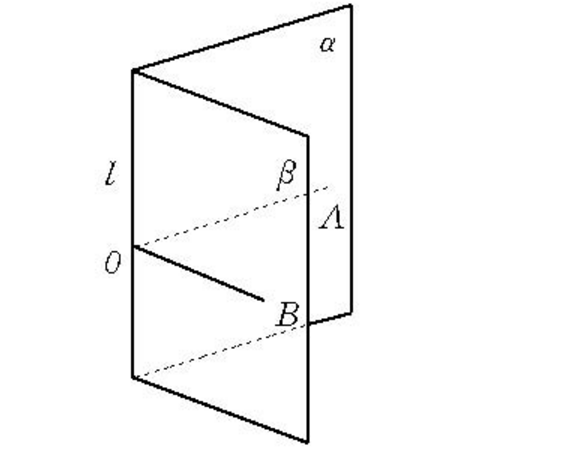
基本介紹
- 中文名：斜二面角
- 外文名：oblique dihedral angle
- 所屬學科：數學
- 所屬問題：立體幾何（二面角）
- 簡介：銳二面角與鈍二面角的統稱
基本介紹,二面角的平面角,
基本介紹
平二面角：兩個面在同一平面內，並且從棱向相反方向伸展而成的二面角，叫做平二面角。
直二面角：(1)平面角是直角的二面角叫做直二面角。(2)如果二面角和它的補二面角相等，則這個二面角叫做直二面角。
優二面角：大於平二面角的二面角叫做優二面角。
劣二面角：小於平二面角的二面角叫做劣二面角。
銳二面角：小於直二面角的二面角叫做銳二面角。
鈍二面角：大於直二面角而小於平二面角的二面角叫做鈍二面角。
斜二面角：銳二面角、鈍二面角統稱斜二面角。
二面角：(1)從一條直線出發的兩個半平面所組成的圖形叫做二面角。這條直線叫做二面角的棱，這兩個半平面叫做二面角的面。(2)有公共直線的兩個半平面組成的圖形，叫做二面角。(3)從一條直線出發的半平面繞著這條直線旋轉，它的最初位置和最後位置所組成的圖形叫做二面角，圖1。
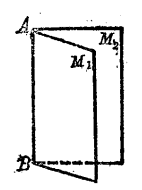圖1表示一個二面角，通常是把表示它的棱的字母寫在中間，表示兩個面的字母寫在兩旁，中間用兩條短橫線隔開(棱用小寫字母表示時可以不用橫線隔開)，如圖中二面角記作“二面角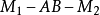
”或“二面角
”，讀作“二面角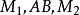
”或二面角“”。
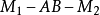
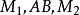
由於“平面角相等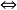
它們的二面角相等”，所以二面角可以用它的平面角來度量，就是說，二面角的平面角是幾度，這個二面角就是幾度。
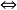
二面角的平面角：以二面角的棱上任意一點為端點，在兩個面內分別作垂直於棱的兩條射線，這兩條射線所成的角叫做二面角的平面角。
平面角相等的二面角相等；相等的二面角的平面角相等。
二面角的內部：二面角把空間分為兩部分，在二面角的兩個面各取一點，得一線段，這線段所在的部分叫做二面角的內部，另一部分，就是不包含這線段的部分，叫做二面角的外部。
二面角的平面角
二面角的平面角是以二面角的棱上任意一點為端點，在兩個面內分別作垂直於棱的兩條射線，這兩條射線所成的角(或叫做線性角)。
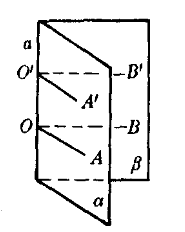圖2如圖，在二面角α-a-β的棱上任取一點O，在半平面α和β內，從點O分別作垂直於棱a的射線OA，OB，射線OA，OB組成∠AOB，在棱a上另取任意一點O′，按同樣方法作∠A′ O′B′，因為OA，OA′和OB，OB′都垂直於棱a，所以∠AOB和∠A′O′B′的兩邊分別平行且方向相同，因此∠AOB=∠A′O′B′，可見，一個二面角的所有平面角都相等，與它們的頂點在棱上的位置無關，因此，對於每一個二面角，其平面角的大小是唯一確定的，於是我們就可以藉助於二面角的平面角來度量二面角的大小。
這個定義與關於二面角大小的直觀印象相一致，若去掉定義中“與棱垂直”的條件，不管改成怎樣的兩條射線，都不會使得兩個面重合的二面角為0°，而且平二面角為180°。
如何尋找並畫出二面角的平面角，在解立體幾何題中起著重要的作用.找出二面角的平面角的方法主要有：
①根據定義求二面角的平面角。
②作二面角的棱的垂面，則垂面和二面角的兩個面的交線所成的角就是該二面角的平面角。
③根據三垂線定理或逆定理作出二面角的平面角。
④根據特殊圖形的性質作，如兩個不共面的等腰三角形若具有公共底邊，則這兩個等腰三角形底邊上的中線的夾角就是這兩個三角形所在平面組成的二面角的平面角。
求二面角大小常用方法：
①先找(作)出二面角的平面角θ，再通過解三角求θ的值；利用面積射影公式：S射=S原·cosθ求二面角θ的大小；
②利用異面直線上兩點間的距離公式；
求解二面角有關問題的過程，也就是綜合運用線線、線面、面面關係(特別是垂直關係)解題過程，計算時要有推理過程，也常用三垂線定理或逆定理，即“一半證明一半算，推證常用三垂線”。
