基本介紹
- 中文名:齊次方程
- 外文名:homogeneous equation
- 類型:齊次線性方程,齊次微分方程
- 學科:數學
- 解法:化為可分離變數的微分方程
- 特點:右端等於零
定義
一
二



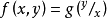
釋義
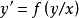




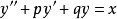
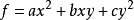
形式


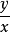

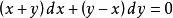
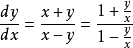
特點解法


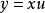
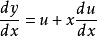




微分方程
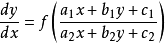


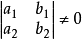
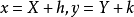


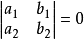

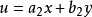





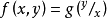
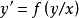




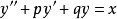
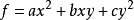


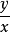

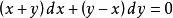
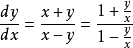


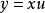
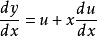




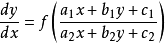


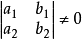
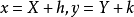


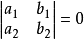

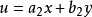

齊次方程(homogeneous equation)是數學的一個方程。指簡化後的方程中所有非零項的指數相等。也叫所含各項關於未知數的次數。其方程左端是含未知數的項,右端等於零...
齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。...
“齊次”從字面上解釋是“次數相等”的意思,是微積分中一個比較常用的概念,英文表達是homogeneous。...
齊次微分方程(homogeneous differential equation)是指能化為可分離變數方程的一類微分方程,它的標準形式是 y'=f(y/x),其中 f 是已知的連續方程。求解齊次微分...
在數學中,齊次函式是一個有倍數性質的函式:如果變數乘以一個係數,則新函式會是原函式再乘上係數的某次方倍。...
在一個線性代數方程中,如果其常數項(即不含有未知數的項)為零,就稱為齊次線性方程...... 方程中,如果其常數項(即不含有未知數的項)為零,就稱為齊次線性方程....
形如y'=f(y/x)的一階微分方程,稱為齊次一階微分方程。齊次微分方程是一個微分方程,如果它的一個解乘以任意常數後,仍是它的解,則稱為齊次微分方程。對一階...
1、關鍵字線性方程乘積的導數中圖分類號O241.6A(x)y′+B(x)y=f(x)A(x)y″+B(x)y′+C(x)y=f(x)等等為線性方程當f(x)≠0時稱為非齊次方程。 ...
三元齊次線性方程組(system of ternary homogeneous linear equations)亦稱三元一次齊次方程組,是一種特殊的線性方程組,即方程組中的各個方程的常數項都是零的三元...
簡單來講,線性微分方程是指關於未知函式及其各階導數都是一次方,否則稱其為非線性微分方程。...
稱為二階常係數線性齊次微分方程;若f(x)≠0,則ay"+by'+cy=f(x)稱為二階常係數線性非齊次微分方程。圖集 二階線性齊次微分方程圖冊 V百科往期回顧 詞條...
齊次坐標就是將一個原本是n維的向量用一個n+1維向量來表示,是指一個用於投影幾何里的坐標系統,如同用於歐氏幾何里的笛卡兒坐標一般。...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
二階常係數線性微分方程是形如y''+py'+qy=f(x)的微分方程,其中p,q是實常數。自由項f(x)為定義在區間I上的連續函式,即y''+py'+qy=0時,稱為二階常...
線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。線性方程...
