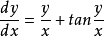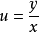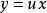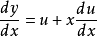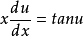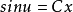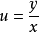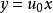齊次微分方程（homogeneous differential equation）是指能化為可分離變數方程的一類微分方程，它的標準形式是 y'=f(y/x)，其中 f 是已知的連續方程。求解齊次微分方程的關鍵是作變換 u=y/x ，即 y=ux ，它可以把方程轉換為關於 u 與 x 的可分離變數的方程，此時有 y'=u+xu'，代入原方程即可得可分離變數的方程 u+xu'=f(u) ,分離變數並積分即可得到結果，需要注意的是，最後應把 u=y/x 代入，並作必要的變形。
基本介紹
- 中文名：齊次微分方程
- 外文名：homogeneous differential equa-lion
- 標準形式：y'=f(y/x)
- 求解關鍵：作變換 u=y/x ，即 y=ux
- 注意事項：最後應把u=y/x代入，並作變形
- 套用學科：高等數學
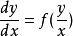
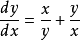
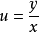
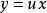
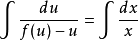
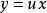
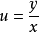
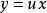
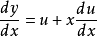
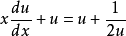
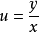
定義,方程特點,方程的解,求解步驟,注意事項,典例,例1,例2,
定義
形如
的一階微分方程稱為齊次微分方程，簡稱微分方程。
方程特點
齊次微分方程的特點是其右端項是以
為變元的連續函式。
例如，
是齊次微分方程，它可以轉化為：
，即
。
方程的解
令
或
，
將其代入
，得：
，
分離變數，得：
兩邊積分，得：
，
求出積分後，再將
回代，便得到方程
的通解。
求解步驟
（1）作變換，將齊次方程轉化為分離變數的微分方程；
（2）求解可分離變數的微分方程；
（3）用
代替步驟（2）中所求通解中的
（即變數還原），就可以得到原方程的通解。
注意事項
典例
例1
求解方程
。
解：令，則，
，
原方程變為：
，即
；
分離變數可得：
，
左右兩端同時積分可得：
，
將 代入，便可得到原方程的通解為：
，其中 C 為任意常數。
例2
求方程
的通解。
解：令，則，，
原方程變為：
，即
；
分離變數可得：
，
左右兩端同時積分可得：
，
將 代入，便可得到原方程的通解為：
，其中 C 為任意常數。
