二次曲面

一般說來，直線與二次曲面相交於兩個點；如果相交於三個點以上，那么此直線全部在曲面上。這時稱此直線為曲面的母線。如果二次曲面被平行平面所截，其截線是二次曲線。通常，我們將三元二次方程所表示的曲面稱作二次曲面。平面叫做一次曲面。

基本介紹

• 中文名：二次曲面
• 外文名：quadratic surface
• 分類：圓柱面 橢圓柱面等
• 截線：二次曲線

簡介

二次曲面是在三維坐標系(x、y、z)下三元二次代數方程對應的所有圖形的統稱。在歐氏三維空間裡坐標x,y,z之間的二次方程（係數為實數，且二次項係數不全為零）所表示的曲面。二次曲面的方程為：

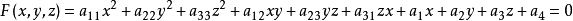
分類

二次曲面有12種：

(1)圓柱面(Cyindrical surface)

(2)橢圓柱面(Elliptic cylinder)

(3)雙曲柱面(Hyperbolic cylinder)

(4)拋物柱面(Parabolic cylinder)

(5)圓錐面(Conical surface)

(6)橢圓錐面(Elliptic cone)

(7)球面(Sphherical surface)

(8)橢球面(Ellipsoid)

(9)橢圓拋物面(Elliptic paraboloid)

(10)單葉雙曲面(Hyperboloid of one sheet)

(11)雙葉雙曲面(Hyperboloid of two sheets)

(12)雙曲拋物面(馬鞍面)(Hyperbolic paraboloid)

最常見的二次曲面是球面和直圓柱面及直圓錐面。此外，二次曲面還包括橢球面、雙曲面（又分為單葉雙曲面和雙葉雙曲面）和拋物面（又分為橢圓拋物面和雙曲拋物面，後者又稱馬鞍面）。當表示二次曲面的一個方程，能分解為兩個一次方程的乘積時，這個二次曲面就退化成兩個或相交或平行或重合的平面。

圓形截線

在二次曲面里，橢圓面、雙曲面、錐面、橢圓拋物面以及橢圓柱面都具有圓形截線。如果某一個平面截二次曲面於一個圓周，則所有平行於它的平面也截該曲面於一個圓周。所以一般來說，二次曲面由兩族平行平面可以截出圓截線。與其平行的切平面的切點是二次曲面的臍點（或圓點）。

二次超曲面

在某個域 K 上的 n 維射影空間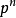 中，射影坐標 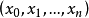滿足方程

（ ，矩陣 是非零的對稱矩陣）的點所構成的集合，稱為 中的二次超曲面，簡稱為二次曲面。

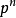
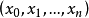
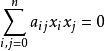
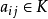
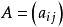
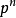
二次曲面的分類問題歸結為二次型的分類問題或 K 上的對稱矩陣的分類問題。設 A 的秩為 r ，則當 K 為複數域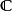 時，二次超曲面的方程可簡化為標準形

當 K 為實數域 時，二次超曲面的方程可簡化為標準形

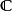
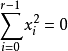
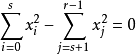
判別法

對於二次曲面的一般式：Ax²+By²+Cz²+2Dyz+2Exz+2Fxy+2Gx+2Hy+2Iz+J=0，

稱為二次曲面的不變數。

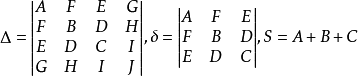
又設

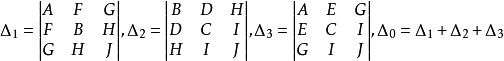
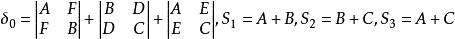
δ>0	Δ=0				點
...	Δ≠0			ΔS>0	虛橢球面
...	...			ΔS<0	橢球面
δ<0	Δ>0				單葉雙曲面
...	Δ=0				二次錐面
...	Δ<0				雙葉雙曲面
δ=0	Δ<0				橢圓拋物面
...	Δ>0				雙曲拋物面
...	Δ=0	δ0>0	Δ0=0		線
...	...	...	Δ0≠0	Δ1*S1+Δ2*S2+Δ3*S3>0	虛橢圓柱面
...	...	...	...	Δ1*S1+Δ2*S2+Δ3*S3<0	橢圓柱面
...	...	δ0<0	Δ0=0		相交平面
...	...	...	Δ0≠0		雙曲柱面
...	...	δ0=0	Δ0≠0		拋物柱面
...	...	...	Δ0=0	G^2+H^2+I^2-JS>0	平行平面
...	...	...	...	G^2+H^2+I^2-JS=0	重合平面
...	...	...	...	G^2+H^2+I^2-JS<0	平行虛平面