橢圓拋物面

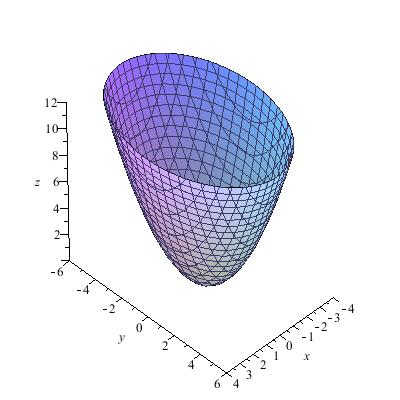
橢圓拋物面是指在同一頂點互相垂直的2個平面的交線上的二條拋物線，其中一條拋物線一邊頂點在別的拋物線上，一邊平面平行地移動時形成的曲面。

基本介紹

• 中文名：橢圓拋物面
• 外文名：Elliptical Paraboloid 
• 形成：拋物線旋轉
• 對稱性：關於z軸對稱
• 套用領域：空間解析幾何
• 套用學科：數學

標準方程

在直角坐標系下，由方程

所表示的曲面叫做橢圓拋物面，方程叫做橢圓拋物面的標準方程，其中a,b是任意的正常數。

由曲面的對稱性可知，橢圓拋物面關於yOz面和zOx面對稱，關於z軸也對稱。

由橢圓拋物線方程可知z ≥0，因此該橢圓拋物面位於xOy面的上方。它與zOx面和yOz面的交線都是拋物線。

性質

(1)曲面的對稱性：橢圓拋物面關於yOx、zOx坐標面以及z軸對稱，但它沒有對稱中心，它與對稱軸交於點(0,0,0)，這點叫做橢圓拋物面的頂點。

(2)曲面與坐標軸的交點：橢圓拋物面通過坐標原點，且除原點外，曲面與三坐標軸沒有別的交點。

(3)曲面的存在範圍：橢圓拋物面全部在髫|9y坐標面的一側，即在z ≥0的一側。

(4)被坐標面截得的曲線：用坐標面y=0,x=0截割曲面，分別得拋物線

這兩個拋物線叫做橢圓拋物面的主拋物線。它們有著相同的頂點和相同的對稱軸，即x軸。開口都向z軸正方形。