定義,由來,通項公式,遞推公式,通項公式內容,通項公式推導,特性,平方與前後項,與集合子集數量的關係,奇數項求和,偶數項求和,平方求和,隔項關係,兩倍項關係,其他公式,套用,與黃金分割比的關係,楊輝三角,矩形面積,質數數量,尾數循環,自然界中“巧合”,數字謎題,影視作品中的斐波那契數列,推廣,斐波那契—盧卡斯數列,廣義斐波那契數列,相關的數學問題,排列組合,兔子繁殖問題,
定義
斐波那契數列是指這樣一個數列:1,1,2,3,5,8,13,21,34,55,89……這個數列從第3項開始 ,每一項都等於前兩項之和。
由來
在數學歷史上,歐洲黑暗時期過後,第一位有影響的數學家是斐波那契(L.Fibonacci,1170一1250)。他早年就隨其父在北非師從阿拉伯人學習算學,後又遊歷地中海沿岸諸國,回義大利後寫成《算經[xq2] 》,也翻譯成《算盤書》。這部很有名的著作主要是一些源自古代中國、印度和希臘的數學問題的匯集,內容涉及整數和分數算法、開方法、二次和三次方程以及不定方程。特別是,在1228年的《算經》修訂版上載有如下“兔子問題”:
如果每對兔子(一雄一雌)每月能生殖一對小兔子(也是一雄 一[xq3] 雌,下同),每對兔子第一個月沒有生殖能力,但從第二個 月[xq4] 以後便能每月生一對小兔子.假定[xq5] 這些兔子都沒有死亡現象,那么從第一對剛出生的兔子開始,12 個月以後會有多少 對[xq6] 兔子呢? 解釋說明為:一個月[xq7] :只有一對兔子;第二個月: 仍然只有一對兔子;第三個月:這對兔子生了一對小兔子, 共有 1+1=2 對兔子.第四個月[xq8] :最初的一對兔子又生一對兔 子,共有 2+1=3 對兔子.則由第一個月到第十二個月兔子的 對數分別是:1,1,2,3,5,8,13,21,34,55,89,144, ……,後 人[xq9] 為了紀念提出兔子繁殖問題的斐波納契, 將這個兔子數 列[xq10] 稱為斐波那契數列, 即把 1,1,2,3,5,8,13,21,34……這樣的數列稱為斐波那契數列。
通項公式
遞推公式
斐波那契數列:1,1,2,3,5,8,13,21,34,55,89…… ,以如下被以遞歸的方法定義:從第三項開始,每一項都等於前兩項之和,顯然這是一個線性遞推數列。
通項公式內容
通項公式推導
上式可化簡得:
那么:
(這是一個以
為首項、以
為末項、
為公比的
等比數列的各項的和)。
所以:
由(1)、(2)式得:
(4)方法四:母函式法
那么有:
不難證明:
因此可以得到:
特性
平方與前後項
從第二項開始(構成一個新數列,第一項為1,第二項為2,……),每個偶數項的平方都比前後兩項之積多1,每個奇數項的平方都比前後兩項之積少1。
如:第二項 1 的平方比它的前一項 1 和它的後一項 2 的積 2 少 1,第三項 2 的
平方比它的前一項 1 和它的後一項 3 的積 3 多 1。
(註:奇數項和偶數項是指
項數的奇偶,而並不是指數列的數字本身的奇偶,比如從數列第二項 1 開始數,第 4 項 5 是奇數,但它是偶數項,如果認為 5 是奇數項,那就誤解題意,怎么都說不通)
與集合子集數量的關係
斐波那契數列的第
n+2項同時也代表了集合
中所有不包含相鄰正整數的
子集個數。
奇數項求和
偶數項求和
平方求和
隔項關係
兩倍項關係
其他公式
套用
與黃金分割比的關係
這樣一個完全是自然數的數列,通項公式是用無理數來表達的。而且當 趨向於無窮大時,前一項與後一項的比值越來越逼近黃金分割0.618(或者說後一項與前一項的比值小數部分越來越逼近 0.618)。
……
……
……
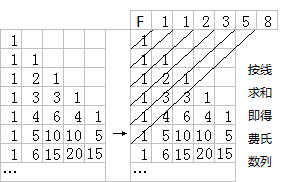
楊輝三角
將
楊輝三角左對齊,成圖1所示排列,將同一斜行的數加起來,即得一數列 1、1、2、3、5、8、……
矩形面積
斐波那契數列與矩形面積的生成相關,由此可以導出一個斐波那契數列的一個性質。
斐波那契數列前幾項的平方和可以看做不同大小的
正方形,由於斐波那契的
遞推公式,它們可以拼成一個大的矩形。這樣所有小正方形的面積之和等於大矩形的面積。則可以得到如下的
恆等式:

質數數量
每3個連續的數中有且只有一個被 2 整除,
每4個連續的數中有且只有一個被 3 整除,
每5個連續的數中有且只有一個被 5 整除,
每6個連續的數中有且只有一個被 8 整除,
每7個連續的數中有且只有一個被 13 整除,
每8個連續的數中有且只有一個被 21 整除,
每9個連續的數中有且只有一個被 34 整除,
.......
我們看到第5、7、11、13、17、23位分別是質數:5,13,89,233,1597,28657(第19位不是)
尾數循環
斐波那契數列的個位數:一個60步的循環:
11235,83145,94370,77415,61785,38190,99875,27965,16730,33695,49325,72910…
進一步,斐波那契數列的最後兩位數是一個300步的循環,最後三位數是一個1500步的循環,最後四位數是一個15000步的循環,最後五位數是一個150000步的循環。
自然界中“巧合”
斐波那契數列表面看來似乎簡單有趣,然而人們發現該數列不僅與黃金分割數,組合數學及機率論等一系列深刻的數學問題關係密切,甚至發現植物枝權與葉序分布、鳳梨紋理與蜂房結構等大量的自然現象也遵從斐波那契數列的奇妙構造。
例如,樹木的生長,由於新生的枝條,往往需要一段“休息”時間,供自身生長,而後才能萌發新枝。所以,一株樹苗在一段間隔,例如一年,以後長出一條新枝;第二年新枝“休息”,老枝依舊萌發;此後,老枝與“休息”過一年的枝同時萌發,當年生的新枝則次年“休息”。這樣,一株樹木各個年份的
枝椏數,便構成斐波那契數列。這個規律,就是生物學上著名的“魯德維格定律”。
其中百合花花瓣數目為 3,
梅花 5 瓣,
飛燕草 8 瓣,
萬壽菊 13 瓣,
向日葵 21 或 34 瓣,
雛菊有 34、55 和 89 三個數目的花瓣。

斐波那契螺旋:在大自然里存在著許多斐波那契螺旋線形態,向日葵花盤有著兩組緊密盤旋的螺旋線,一組按照順時針旋轉的數目為21,另一組按照逆時 針旋轉的數目為3 4,正 好是斐波 那契數列中相鄰的兩個 數且比值接近黃金分割比,而且排列的種子以中心為點四面發散形成的角度接近於黃金角;銀河系中的四條主旋臂旋轉分開組成大約為12度的角度,它所反映出來的螺旋形狀和斐波那契螺旋線幾乎完全相同;鸚鵡螺外殼截面形狀為典型的斐波那契螺旋形,被認為是以斐氏數列形成的最完美的螺旋線。
事實上許多常見的植物,如我們食用的青菜、包心菜、芹菜等的葉子排列也具有這個特性。儘管這些順逆螺旋的數目並不固定,但它們也並不隨機,它們是斐波那契序列中的相鄰數字。
這些植物懂得斐波那契數列嗎?當然並非如此,它們只是按照自然的規律才進化成這樣。這似乎是植物排列種子的“最佳化方式”,它能使所有種子具有差不多的大小空間卻又疏密得當,不至於在圓心處擠了太多的種子而在圓周處卻又稀稀拉拉。葉子的生長方式也是如此,對於許多植物來說,每片葉子從中軸附近生長出來,為了在生長的過程中一直都能最佳地利用空間(要考慮到葉子是一片一片逐漸地生長出來,而不是一下子同時出現的),每片葉子和前一片葉子之間的角度應該是222.5度,這個角度被稱為“黃金角度”,因為它和整個圓周360度之比是黃金分割數1.618033989⋯⋯的倒數,而這種生長方式就決定了斐波那契螺旋的產生。向日葵的種子排列形成的斐波那契螺旋有時能達到89條,甚至144條。
數字謎題
三角形的三邊關係定理和斐波那契數列的一個聯繫:
現有長為 144 cm 的鐵絲,要截成n小段(n≥3),每段的長度不小於 1 cm,如果其中任意三小段都不能拼成三角形,則n的最大值為:
由於形成三角形的充要條件是任何兩邊之和大於第三邊,因此不構成三角形的條件就是存在兩邊之和不超過另一邊。截成的鐵絲最小為 1,因此可以放 2 個 1,第三條線段就是 2(為了使得n最大,因此要使剩下來的鐵絲儘可能長,因此每一條線段總是前面的相鄰2段之和),依次為:1、1、2、3、5、8、13、21、34、55,以上各數之和為 143,與 144 相差 1,因此可以取最後一段為 56,這時 n 達到最大為 10。
我們看到,“每段的長度不小於 1”這個條件起了控制全局的作用,正是這個最小數1 產生了斐波那契數列,如果把 1 換成其他數,遞推關係保留了,但這個數列消失了。這裡,三角形的三邊關係定理和斐波那契數列發生了一個聯繫。
在這個問題中,這個143是斐波那契數列的前
項和,我們是把144超出143的部分加到最後的一個數上去,如果加到其他數上,就有3條線段可以構成三角形了。
影視作品中的斐波那契數列
斐波那契數列在歐美可謂是盡人皆知,於是在電影這種通俗藝術中也時常出現,比如在風靡一時的《達文西密碼》里它就作為一個重要的符號和情節線索出現,在《魔法玩具城》里又是在店主招聘會計時隨口問的問題。可見此數列就像黃金分割一樣流行。可是雖說叫得上名,多數人也就背過前幾個數,並沒有深入理解研究。在電視劇中也出現斐波那契數列,比如:日劇《考試之神》第五回,義嗣做全國模擬考試題中的最後一道數學題~在FOX 熱播美劇《Fringe》中更是無數[xq1] 次引用,甚至作為全劇宣傳海報的設計元素之一。
推廣
斐波那契—盧卡斯數列
盧卡斯數列 1、3、4、7、11、18…,也具有斐波那契數列同樣的性質。(我們可稱之為斐波那契—盧卡斯遞推:從第三項開始,每一項都等於前兩項之和
)
類似的數列還有無限多個,我們稱之為斐波那契—盧卡斯數列。
如1,4,5,9,14,23…,因為1,4開頭,可記作F[1,4],斐波那契數列就是F[1,1],盧卡斯數列就是F[1,3],斐波那契—盧卡斯數列就是F[a,b]。
斐波那契—盧卡斯數列之間的廣泛聯繫:
①任意兩個或兩個以上斐波那契—盧卡斯數列之和或差仍然是斐波那契—盧卡斯數列。
如:F[1,4]n+F[1,3]n=F[2,7]n,F[1,4]n-F[1,3]n=F[0,1]n=F[1,1](n-1),
②任何一個斐波那契—盧卡斯數列都可以由斐波那契數列的有限項之和獲得,如
黃金特徵與孿生斐波那契—盧卡斯數列
斐波那契—盧卡斯數列的另一個共同性質:中間項的
平方數與前後兩項之積的差的
絕對值是一個恆值,
盧卡斯數列:|3*3-1*4|=|4*4-3*7|=…=5
F[1,4]數列:|4*4-1*5|=11
F[2,5]數列:|5*5-2*7|=11
F[2,7]數列:|7*7-2*9|=31
斐波那契數列這個值是1最小,也就是前後項之比接近
黃金比例最快,我們稱為黃金特徵,黃金特徵1的數列只有斐波那契數列,是獨生數列。盧卡斯數列的黃金特徵是5,也是獨生數列。前兩項
互質的獨生數列只有斐波那契數列和盧卡斯數列這兩個數列。
而F[1,4]與F[2,5]的黃金特徵都是11,是孿生數列。F[2,7]也有孿生數列:F[3,8]。其他前兩項
互質的斐波那契—盧卡斯數列都是孿生數列,稱為孿生斐波那契—盧卡斯數列。
廣義斐波那契數列
斐波那契數列的黃金特徵1,還讓我們聯想到
佩爾數列:1,2,5,12,29,…,也有|2*2-1*5|=|5*5-2*12|=…=1(該類數列的這種
特徵值稱為勾股特徵)。
據此類推到所有根據前兩項導出第三項的通用規則:
,稱為廣義斐波那契數列。
當
時,我們得到佩爾—勾股弦數(跟邊長為整數的
直角三角形有關的數列集合)。
當
時,我們得到
等差數列。其中
時,我們得到
自然數列1,2,3,4,5…自然數列的特徵就是每個數的平方與前後兩數之積的差為 1(等差數列的這種差值稱為自然特徵)。
具有類似黃金特徵、勾股特徵、自然特徵的廣義——斐波那契數列
。
相關的數學問題
排列組合
有一段樓梯有10級台階,規定每一步只能跨一級或兩級,要登上第 10 級台階有幾種不同的走法?
這就是一個斐波那契數列:登上第一級台階有一種登法;登上兩級台階,有兩種登法;登上三級台階,有三種登法;登上四級台階,有五種登法……
1,2,3,5,8,13…… 所以,登上十級,有 89 種走法。
類似的,一枚均勻的硬幣擲10次,問
不連續出現正面的可能情形有:
兔子繁殖問題
一般而言,兔子在出生兩個月後,就有繁殖能力,一對兔子每個月能生出一對小兔子來。如果所有兔子都不死:
我們不妨拿新出生的一對小兔子分析一下:
第一個月小兔子沒有繁殖能力,所以還是一對
三個月以後,老兔子又生下一對,因為小兔子還沒有繁殖能力,所以一共是三對……
依次類推可以列出下表:
幼仔對數=前月成兔對數
成兔對數=前月成兔對數+前月幼仔對數
總體對數=本月成兔對數+本月幼仔對數
可以看出幼仔對數、成兔對數、總體對數都構成了一個數列。這個數列有關十分明顯的特點,那是:前面相鄰兩項之和,構成了後一項,即斐波那契數列。