等比故事
根據歷史傳說記載,西洋棋起源於
古印度,至今見諸於文獻最早的記錄是在
薩珊王朝時期用波斯文寫的.據說,有位印度教宰相見國王自負虛浮,決定給他一個教訓.他向國王推薦了一種在當時尚無人知曉的遊戲.國王當時整天被一群溜須拍馬的大臣們包圍,百無聊賴,很需要通過遊戲方式來排遣鬱悶的心情.
國王對這種新奇的遊戲很快就產生了濃厚的興趣,高興之餘,他便問那位宰相,作為對他忠心的獎賞,他需要得到什麼賞賜.宰相開口說道:請您在棋盤上的第一個格子上放1粒麥子,第二個格子上放2粒,第三個格子上放4粒,第四個格子上放8粒……即每一個次序在後的格子中放的麥粒都必須是前一個格子麥粒數目的兩倍,直到最後一個格子第64格放滿為止,這樣我就十分滿足了。“好吧!”國王哈哈大笑,慷慨地答應了宰相的這個謙卑的請求。
這位聰明的宰相到底要求的是多少麥粒呢?稍微算一下就可以得出:1+2+2^2+2^3+2^4+……+2^63=2^64-1,直接寫出數字來就是18,446,744,073,709,551,615粒,這位宰相所要求的,竟是全世界在兩千年內所產的小麥的總和!
如果造一個寬四米,高四米的糧倉來儲存這些糧食,那么這個糧倉就要長三億千米,可以繞地球赤道7500圈,或在日地之間打個來回。
國王哪有這么多的麥子呢?他的一句慷慨之言,成了他欠宰相西薩·班·達依爾的一筆永遠也無法還清的債。
正當國王一籌莫展之際,
王太子的數學教師知道了這件事,他笑著對國王說:“陛下,這個問題很簡單啊,就像1+1=2一樣容易,您怎么會被它難倒?”國王大怒:“難道你要我把全世界兩千年產的小麥都給他?”年輕的教師說:“沒有必要啊,陛下。其實,您只要讓宰相大人到糧倉去,自己數出那些麥子就可以了。假如宰相大人一秒鐘數一粒,數完18,446,744,073,709,551,615粒麥子所需要的時間,大約是5800億年(大家可以自己用
計算器算一下!)。就算宰相大人日夜不停地數,數到他自己魂歸極樂,也只是數出了那些麥粒中極小的一部分。這樣的話,就不是陛下無法支付賞賜,而是宰相大人自己沒有能力取走賞賜。”國王恍然大悟,當下就召來宰相,將教師的方法告訴了他。
西薩·班·達依爾沉思片刻後笑道:“陛下啊,您的智慧超過了我,那些賞賜……我也只好不要了!”當然,最後宰相還是獲得了很多的賞賜。
公式
(1)定義式:
 合併圖冊
合併圖冊(2)
通項公式(等比數列通項公式通過定義式疊乘而來):
(3)求和公式:
求和公式用文字來描述就是:Sn=首項(1-公比的n次方)/1-公比(公比≠1)如果公比q=1,則等比數列中每項都相等,其通項公式為
,任意兩項
,
的關係為
;在運用等比數列的前n項和時,一定要注意
討論公比q是否為1.(4)從等比數列的定義、通項公式、前n項和公式可以推出:
記πn=a1·a2…an,則有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1。
另外,一個各項均為
正數的等比數列各項取同
底數後構成一個
等差數列;反之,以任一個正數C為底,用一個等差數列的各項做
指數構造冪Can,則是等比數列。在這個意義下,我們說:一個正項等比數列與等差數列是“同構”的。
等比中項定義:從第二項起,每一項(
有窮數列的末項除外)都是它的前一項與後一項的等比中項。
(6)無窮遞縮等比數列各項和公式:
無窮遞縮等比數列各項和公式:公比的絕對值小於1的
無窮等比數列,當n無限增大時的極限叫做這個無窮等比數列各項的和。
(7)由等比數列組成的新的等比數列的公比:{an}是公比為q的等比數列
1.若A=a1+a2+……+an
B=an+1+……+a2n
C=a2n+1+……a3n
則,A、B、C構成新的等比數列,公比Q=q^n
2.若A=a1+a4+a7+……+a3n-2
B=a2+a5+a8+……+a3n-1
C=a3+a6+a9+……+a3n
則,A、B、C構成新的等比數列,公比Q=q。
性質
(1)若m、n、p、q∈N*,且m+n=p+q,則am*an=ap*aq。
(2)在等比數列中,依次每k項之和仍成等比數列。
(3)若“G是a、b的
等比中項”則“G^2=ab(G≠0)”。
(4)若{an}是等比數列,公比為q1,{bn}也是等比數列,公比是q2,則{a2n},{a3n}…是等比數列,公比為q1^2,q1^3…{can},c是
常數,{an*bn},{an/bn}是等比數列,公比為q1,q1q2,q1/q2。
(5)若(an)為等比數列且各項為正,公比為q,則(log以a為底an的
對數)成等差,公差為log以a為底q的對數。
(6)等比數列前n項之和Sn=A1(1-q^n)/(1-q)=A1(q^n-1)/(q-1)=(A1q^n)/(q-1)-A1/(q-1)
在等比數列中,首項A1與公比q都不為零。
(7)由於首項為a1,公比為q的等比數列的通項公式可以寫成an=(a1/q)*q^n,它的
指數函式y=a^x有著密切的聯繫,從而可以利用指數函式的性質來研究等比數列。
求通項方法
(1)待定
係數法:已知a(n+1)=2an+3,a1=1,求an?
構造等比數列a(n+1)+x=2(an+x)
a(n+1)=2an+x,∵a(n+1)=2an+3 ∴x=3
∴(a(n+1)+3)/(an+3)=2
∴{an+3}為首項為4,公比為2的等比數列,所以an+3=a1*q^(n-1)=4*2^(n-1),an=2^(n+1)-3
(2)定義法:已知Sn=a·2^n+b,,求an的通項公式?
∵Sn=a·2^n+b∴Sn-1=a·2^n-1+b
∴an=Sn-Sn-1=a·2^n-1。
套用
生活中的套用
等比數列在生活中也是常常運用的。如:銀行有一種支付利息的方式——
複利。即把前一期的利息和
本金加在一起算作本金,在計算下一期的利息,也就是人們通常說的“利滾利”。按照複利計算本利和的公式:本利和=本金*(1+利率)^存期。
隨著房價越來越高,很多人沒辦法像這樣一次性將房款付清,總是要向銀行借錢,既可以申請公積金也可以申請銀行貸款,但是如果還款到一定時間後想了解自己還得還多少本金時,也可以利用數列來自己計算。眾所周知,按揭貸款(公積金貸款)中一般實行按月等額還本付息。下面就來尋求這一問題的解決辦法。若貸款數額 a0 元,貸款月利率為 p,還款方式每月等額還本付息 a 元,設第 n 月還款後的本金為 an,那么有:a1=a0(1+p)-a;a2=a1(1+p)-a;a3=a2(1+p)-a;......an+1=an(1+p)-a,.... 將其變形,得(an+1-a/p)/(an-a/p)=1+p。由此可見,{an-a/p} 是一個以 a1-a/p 為首項,1+p 為公比的等比數列。
其實類似的還有零存整取、整存整取等銀行儲蓄借貸,甚至還可以延伸到生物界的細胞細胞分裂。
數學中的套用
例1
設ak,al,am,an是等比數列中的第k、l、m、n項,若k+l=m+n,求證:ak*al=am*an
證明:設等比數列的首項為a1,公比為q,則:
ak=a1·q^(k-1),al=a1·q^(l-1),am=a1·q^(m-1),an=a1·q^(n-1)
所以:
ak*al=a^2*q^(k+l-2),am*an=a^2*q(m+n-2),
故:ak*al=am*an
說明:這個例題是等比數列的一個重要性質,它在解題中常常會用到。它說明等比數列中距離兩端(首末兩項)距離等遠的兩項的乘積等於首末兩項的乘積,即:
a(1+k)·a(n-k)=a1·an
對於等差數列,同樣有:在等差數列中,距離兩端等這的兩項之和等於首末兩項之和。即:
a(1+k)+a(n-k)=a1+an。
例2
在等差數列中,a4+a6+a8+a10+a12=120,則2a9-a10=( )
A.20 B.22 C.24 D28
解:由a4+a12=2a8,a6+a10 =2a8及已知條件得:
5a8=120,a8=24
而2a9-a10=2(a1+8d)-(a1+9d)=a1+7d=a8=24。
故選C。
例3
設Sn為等差數列的前n項之和,S9=18,a(n-4)=30(n>9),Sn=336,則n為( )
A.16 B.21 C.9 D.8
解:由於S9=9×a5=18,故a5=2,所以a5+a(n-4)=a1+an=2+30=32,而,故n=21選B。
例4
設等差數列滿足3a8=5a13,且a1>0,Sn為其前n項之和,則Sn(n∈N*)中最大的是( )。 (1995年全國高中聯賽第1題)
(A)S10 (B)S11 (C)S20 (D)S21
解:∵3a8=5a13
∴3(a1+7d)=5(a1+12d)
故a1=-19.5d
令an≥0→n≤20;當n>20時an<0
∴S19=S20最大,選(C)
例5
將正奇數
集合{1,3,5,…}由小到大按第n組有(2n-1)個奇數進行分組:
{1}, {3,5,7},{9,11,13,15,17},…
(第一組) (第二組) (第三組)
則1991位於第_____組中。
【1991年全國高中數學聯賽第3題】
解:依題意,前n組中共有奇數
1+3+5+…+(2n-1)=n^2個
而1991=2×996-1,它是第996個正奇數。
∵31^2=961<996<1024=32^2
∴1991應在第31+1=32組中。
故填32。

 合併圖冊
合併圖冊





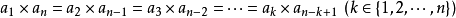








 合併圖冊
合併圖冊