基本介紹
- 中文名:等比差數列
- 外文名:geometric-arithmetic progression
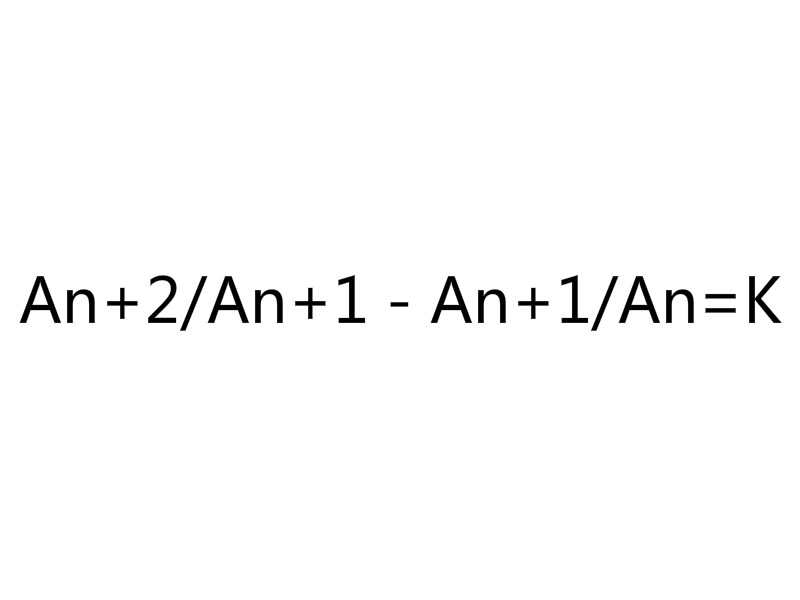
若數列滿足an+2/an+1-an+1/an=k(k為常數),則稱該數列為等比差數列,其中k為公比差。... 關於等比差數列的定義說法不一,有人認為,其概念應為:一個首項...
等比數列公式就是在數學上求一定數量的等比數列的和的公式。另外,一個各項均為正數的等比數列各項取同底數數後構成一個等差數列;反之,以任一個正數C為底,用一...
等比數列求和公式是求等比數列之和的公式。如果一個數列從第2項起,每一項與它的前一項的比等於同一個常數,這個數列就叫做等比數列。這個常數叫做等比數列的公比,...
等比數列是指從第二項起,每一項與它的前一項的比值等於同一個常數的一種數列,常用G、P表示。這個常數叫做等比數列的公比,公比通常用字母q表示(q≠0),等比數列...
等差數列是指從第二項起,每一項與它的前一項的差等於同一個常數的一種數列,常用A、P表示。這個常數叫做等差數列的公差,公差常用字母d表示。例如:1,3,5,7,9...
對於一個數列 {an},如果任意相鄰兩項之商(即二者的比)為一個常數,那么該數列為等比數列,且稱這一定值商為公比 q ;從第一項a1 到第n項an 的總和,記為Tn...
數列求和阿貝爾求和公式 編輯 該公式又叫做分部求和公式,是離散型的分部積分法,最早由數學家阿貝爾提出。這個方法也適合解決等差等比數列相乘的數列求和,但比起上面的...
如果一個數列從第2項起,每一項與它的前一項的比等於同一個常數,且每一項都不為0(常數),這個數列就叫做等比數列。這個常數叫做等比數列的公比,公比通常用字母q...
5 等差數列 ▪ 定義 ▪ 通項公式 ▪ 等差中項 ▪ 前n項和 ▪ 性質 ▪ 套用 6 等比數列 ▪ 定義 ▪ 等比中項 ▪ 通項公式...
做差數列,指的是數列經過一次做差或者多次做差之後,得到一個有規律的基本數列的數列,通常來說,基本數列可以是常數列、等差數列、等比數列、平方數列、質數數列等等...
一個常數數列如:2,2,2,2,2,2,...一定是首項為a,公差為0的等差數列。所有常數數列(除an=0外)均是首項為a,公比為1的等比數列。常數數列的實質就是零階...
數列,a,aq,aq^2……aq^n。我們把|q|<1無窮等比數列稱為無窮遞縮等比數列,它的前n項和的極限才存在,當|q|≥1無窮等比數列它的前n項和的極限是不存在的...
等差數列指的是數列的相鄰數值差值是一個常數,如1、3、5、7、9,其公差為2。3、等比數列等比數列指的是數列相鄰數值的比值是一個常數,如1、3、9、27、81,...
等差數列的遞推公式: (d為公差)等比數列的遞推公式: (q為公比)遞推公式概念遞推公式的概念:可以通過給出數列(按一定次序排列的一列數稱為數列(sequence of ...
《數列·遞推·遞歸》是該叢書中的一種.它從數列的概念和最基本的數列——等差數列和等比數列研究開始,分別 對與等差數列、等比數列有關的差分數列、等比差數列...
一個數列相鄰的兩項作差,得到的新數列是一個基本數列,則稱原數列為二級數列。新數列可能是等差數列、等比數列、質數數列、周期數列、對稱數列、冪數列等基本數列...
第一章 等差、等比數列概念和性質 1 一、數列的概念 1 二、等差數列的定義和通項公式 5 三、等差數列求和 8 四、等差數列的性質 12 五、等比數列的...
形如An=BnCn,其中{Bn}為等差數列,通項公式為bn=b1+(n-1)*d;{Cn}為等比數列,通項公式為cn=c1*q^(n-1);對數列An進行求和,首先列出Sn,記為式(1);...
1 遞推列 2 等比數列 3 等比公式 4 等差數列 概念如果一個數列的第n項an與該數列的其他一項或多項之間存在對應關係的,這個關係就稱為該數列的遞推公式。...
