基本介紹
- 中文名:通項公式
- 外文名:general formulas
- 特點:不唯一
- 反例:所有質數組成的數列
- 舉例:等差數列,等比數列
- 學科:數學
定義





性質
- 若已知一個數列的通項公式,那么只要依次用1,2,3,...去代替公式中的n,就可以求出這個數列的各項。
- 不是任何一個無窮數列都有通項公式,如所有的質數組成的數列就沒有通項公式。
- 給出數列的前n項,通項公式不唯一。
- 有的數列的通項可以用兩個或兩個以上的式子來表示。
等差數列通項公式
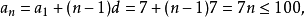






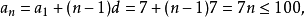

如果數列{an}的第n項an與n之間的關係可以用一個公式來表示,這個公式叫做數列的通項公式(general formulas)。有的數列的通項可以用兩個或兩個以上的式子來表示。...
按一定次序排列的一列數稱為數列,而將數列{an} 的第n項用一個具體式子(含有參數n)表示出來,稱作該數列的通項公式。這正如函式的解析式一樣,通過代入具體的n...
對稱數列的通項公式:對稱數列總的項數個數:用字母s表示對稱數列中項:用字母C表示等差對稱數列公差:用字母d表示等比對稱數列公比:用字母q表示...
等列公式 [1] :an=a1+(n-1)d,(n為正整數)S1為首項,an為第n項的通項公式,d為公差。前n項和公式為:Sn=na1+n(n-1)d/2,(n為正整數)...
素數公式通項公式 編輯 n的點集分兩組,一組為偽素數的變數集,一組為素數的變數集合,其中偽素數的變數集合有以下方程式來確定:素數變數n(x,y)的充分必要條件為...
數列的通項與遞推公式是按一定次序排列的一列數稱為數列(sequence of number)。數列中的每一個數都叫做這個數列的項。排在第一位的數稱為這個數列的第1項(...
(3)從等比數列的定義、通項公式、前n項和公式可以推出: ,k∈{1,2,…,n}(4)等比中項:當r滿足p+q=2r時,那么則有 ,即 為 與 的等比中項。...
等比數列求和公式是求等比數列之和的公式。如果一個數列從第2項起,每一項與它的前一項的比等於同一個常數,這個數列就叫做等比數列。這個常數叫做等比數列的公比,...
(2n-1)。等差數列{an}的通項公式為:an=a1+(n-1)d。前n項和公式為:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。注意: 以上n均屬於正整數。...
有趣的是,這樣一個完全是自然數的數列,通項公式卻是用無理數來表達的。而且當n趨向於無窮大時,前一項與後一項的比值越來越逼近黃金分割0.618(或者說後一項與...
(4)從等比數列的定義、通項公式、前n項和公式可以推出:(5)等比中項:若 ,那么 為 等比中項。記πn=a1·a2…an,則有π2n-1=(an)2n-1,π2n+1=(an+...
已知a1=1,a2=1,an=a(n-1)+a(n-2)(n>=3),求數列{an}的通項公式。解:設an-αa(n-1)=β(a(n-1)-αa(n-2))。得α+β=1。...
2n-1。通項公式為:an=a1+(n-1)*d。首項a1=1,公差d=2。前n項和公式為:Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2。注意:以上n均屬於正...
求二項式展開式係數的問題,實際上是一種組合數的計算問題. 用係數通項公式來計算,稱為“式算”;用楊輝三角形來計算,稱作“圖算”....
數列求和對按照一定規律排列的數進行求和。求Sn實質上是求{Sn}的通項公式,應注意對其含義的理解。常見的方法有公式法、錯位相減法、倒序相加法、分組法、裂項法、...
數列遞推公式特點:1)有些數列的遞推公式可以有不同形式,即不唯一。2)有些數列沒有遞推公式,即有遞推公式不一定有通項公式。數列等差數列 編輯 ...
,通項公式為 其中, 叫做二項式係數。等號右邊的多項式叫做二項展開式。其i項係數可表示為 ,即n取i的組合數目。 因此係數亦可表示為帕斯卡三角形(Pascal's Triang...
有通項公式的數列只是少數,研究遞推數列公式給出數列的方法可使我們研究數列的範圍大大擴展。新大綱關於遞推數列規定的教學目標是“了解遞推公式是給出數列的一種...
通項公式 套用 編程 基本判斷思路 代碼 素性檢測 篩素數法 猜想 孿生素數無限多的證明 一。陰性合數定理和陰性素數定理 二。陽性合數定理和陽性素數定理 三。與孿...
