基本介紹
- 中文名:等差數列求和公式
- 外文名:sequence of number
- 套用學科:高中數學、計算機
- 適用領域範圍:數據運算
- 適用領域範圍:數學計算
一般定義
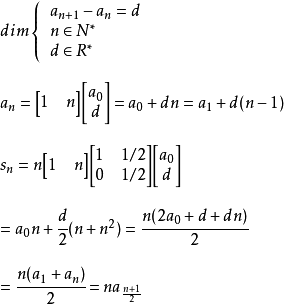
擴展:多項式數列
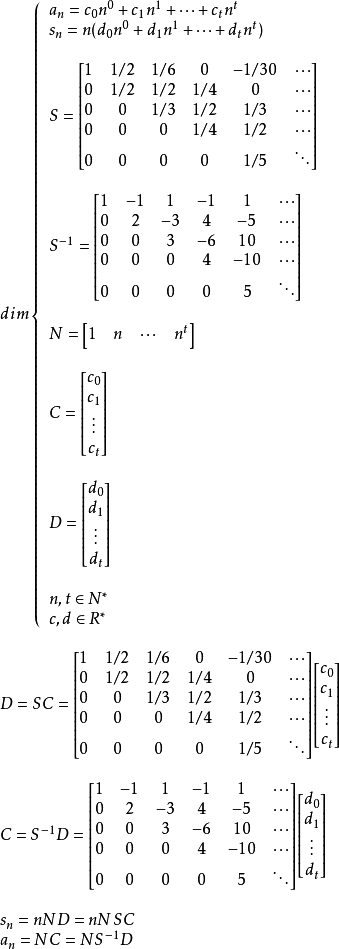
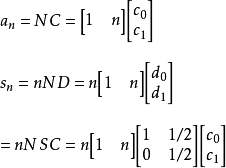
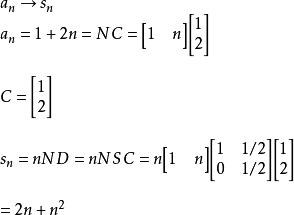
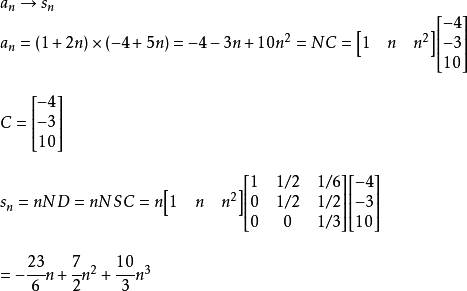
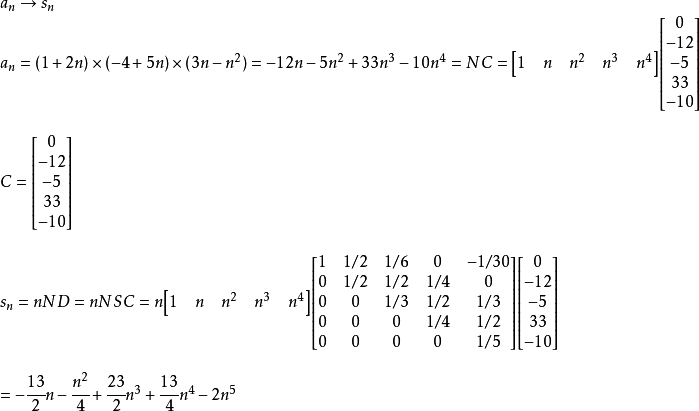

凱森和
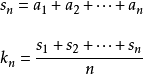
多項式數列高階和
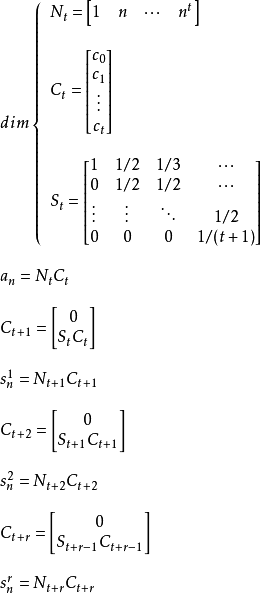
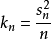
其他結論
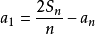
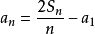
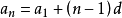
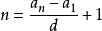
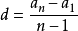
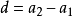
特殊性質
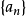
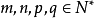
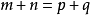
求和公式
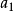
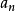

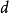

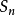
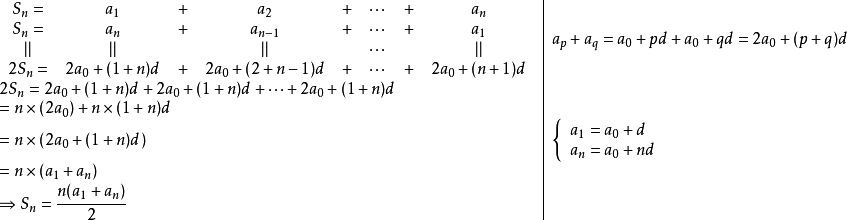
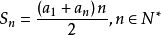
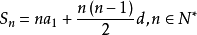
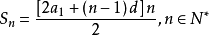
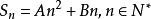
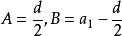
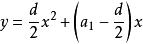

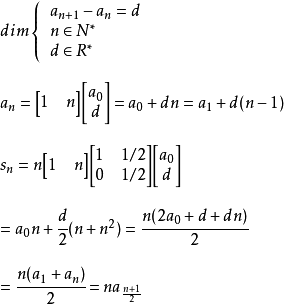
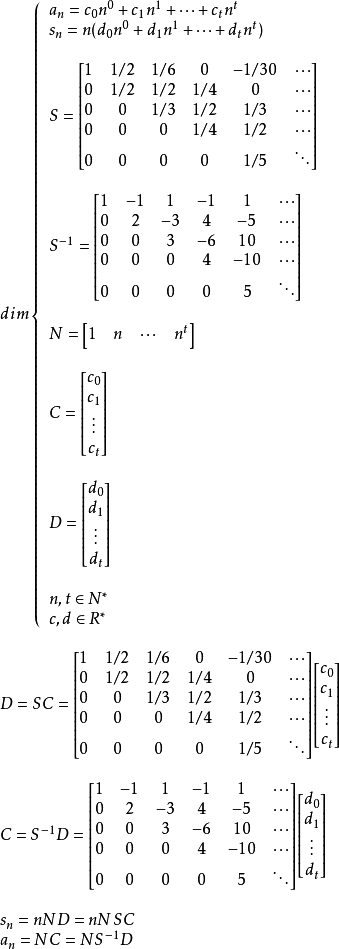
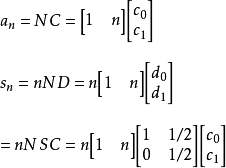
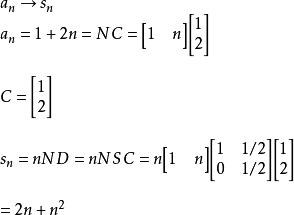
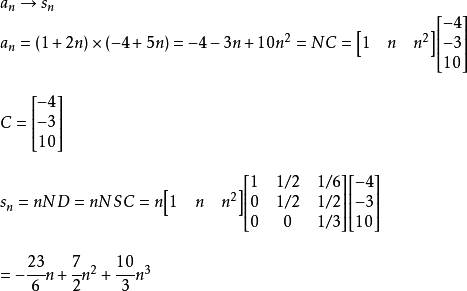
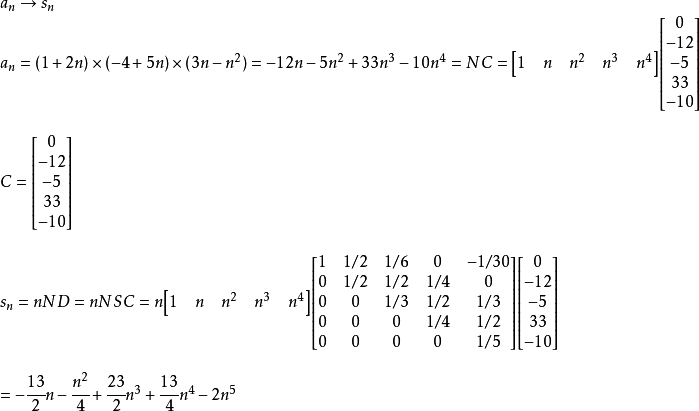

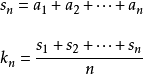
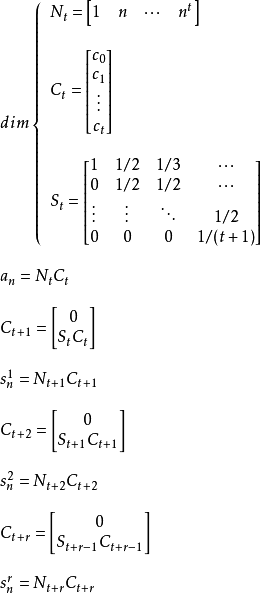
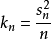
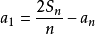
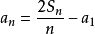
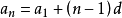
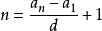
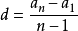
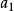
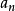
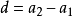
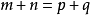
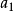
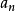

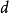

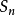
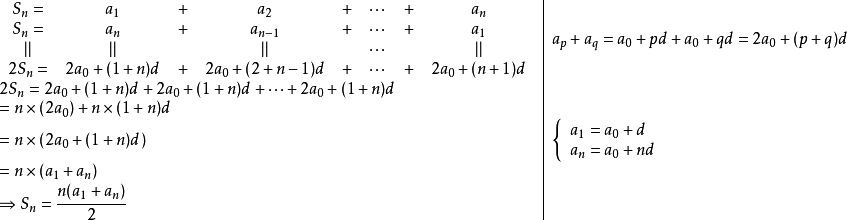
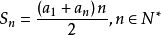
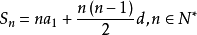
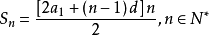
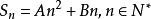
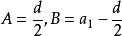
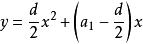
等差數列求和公式編輯 鎖定 討論999 本詞條由“科普中國”科學百科詞條編寫與套用工作項目 審核。等差數列是常見數列的一種,可以用AP表示,如果一個數列從第二項起...
前n項和公式為:Sn=a1*n+[n*(n-1)*d]/2 Sn=[n*(a1+an)]/2 Sn=d/2*n²+(a1-d/2)*n 注:以上n均屬於正整數。 等差數列公式包括:求和、通項...
數列求和對按照一定規律排列的數進行求和。求Sn實質上是求{Sn}的通項公式,應注意對其含義的理解。常見的方法有公式法、錯位相減法、倒序相加法、分組法、裂項法、...
注意:n是正整數(相當於n個等差中項之和)。等差數列前N項求和,實際就是梯形公式的妙用:上底為a1首項,下底為a1+(n-1)d,高為n。即:[a1+a1+(n-1)d]...
等差數列1.通項公式差為d的n項為:An=A1+(n-1)d2.等差求和公式Sn=(A1+An)n/2Sn=n(A1)+ n(n-1)d/2詞條標籤: 科學, 學科 ...
等差數列即當bn公比為1時差比數列的特殊形式,等比數列即當an公差為0時差比數列的特殊形式.差比數列的性質,就是由成倍遞增的一組數所組成的數列.求和公式,可用...
對於一個數列{ an },如果任意相鄰兩項之差為一個常數,那么該數列為等差數列,...遞推公式為 ,且f(n)可以求和例:數列{an},滿足a1=1/2,an+1 = an + 1...
數列求和方法,數學上的一種求數列的一些方法。...... 數列求和方法,數學上的一種求數列的一些方法。...6、在等差數列 中,有關Sn 的最值問題——常用鄰項...
自然數冪求和公式,是李善蘭先生提出的一種數列求和公式。它的提出在中國數學史上有重要地位。...
等比數列公式就是在數學上求一定數量的等比數列的和的公式。另外,一個各項均為正數的等比數列各項取同底數數後構成一個等差數列;反之,以任一個正數C為底,用一...
等差數列求和公式:和=(首項+末項)*項數/2,求和Word方法 編輯 以Microsoft Word 2003軟體為例介紹Word表格中求和計算的方法:第1步,根據實際情況將需要計算的數據...
裂項法,這是分解與組合思想在數列求和中的具體套用。是將數列中的每項(通項)...6、在等差數列 中,有關Sn 的最值問題——常用鄰項變號法求解:...
