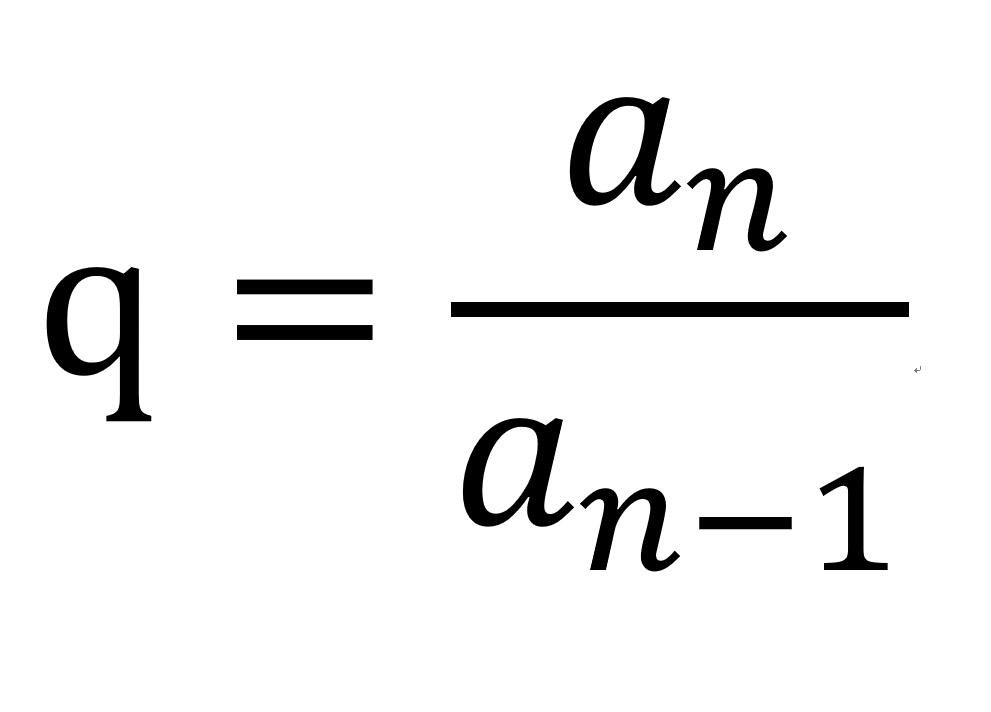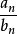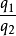公比

公比是對於等比數列這一特殊數列而言的，它是指在等比數列中後一項與前一項的商。

基本介紹

• 中文名：公比
• 外文名：Common ratio
• 符號：q
• 公式：an/a(n-1)
• 套用領域：數理科學

術語簡介

公比(Common ratio)是對於等比數列這一特殊數列而言的,是在等比數列中後一項與前一項的商；或者說每一項與它的前一項的比都等於的同一個常數，這個常數就是公比。

等比數列的公比符號為：q

等比數列的公比公式為：。

詳細內容

等比數列

如果一個數列從第2項起，每一項與它的前一項的比等於同一個常數，這個數列就叫做等比數列。這個常數叫做等比數列的公比，公比通常用字母q表示。

（1）等比數列的通項公式是：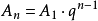

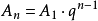
若通項公式變形為(n∈N*)，當q>0時，則可把看作自變數n的函式，點(n，)是曲線上的一群孤立的點。

（2）求和公式： (q=1時)

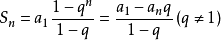
任意兩項，的關係為

（3）從等比數列的定義、通項公式、前n項和公式可以推出：，k∈{1,2,…,n}

（4）等比中項：，則為、等比中項。

另外，一個各項均為正數的等比數列各項取同底數後構成一個等差數列；反之，以任一個正數C為底，用一個等差數列的各項做指數構造冪Can，則是等比數列。在這個意義下，我們說：一個正項等比數列與等差數列是“同構”的。

性質

①若 m、n、p、q∈N*，且m+n=p+q，則。

②在等比數列中，依次每 k項之和仍成等比數列。

③若（）是等比數列，公比為，（）也是等比數列，公比是，則

（），（）…是等比數列，公比為，…

（c），c是常數，（*），（)是等比數列，公比為，，。

在等比數列中，首項與公比q都不為零。

注意：上述公式中表示A的n次方。

由於首項為a1，公比為q的等比數列的通向公式可以寫成，它的指數函式y=a^x有著密切的聯繫，從而可以利用指數函式的性質來研究等比數列。

編輯本段等比數列的套用

等比數列在生活中也是常常運用的。

如：銀行有一種支付利息的方式——複利。

即把前一期的利息赫本金價在一起算作本金，

在計算下一期的利息，也就是人們通常說的利滾利。

按照複利計算本利和的公式：本利和=本金*(1+利率)^存期。