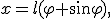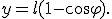數學物理反問題

數學物理反問題是源於物理、生物、醫學、地質等眾多科學領域中的實際問題，經過數學建模而產生的一個新興交叉學科領域。 顧名思義，反問題是相對於正問題而言的。“盲人聽鼓”反問題為例，它的正問題就是要在已知鼓的形狀的條件下，研究其發聲規律，這在數學物理歷史上已經研究在先，而且比較成熟。此時鼓的所有譜都能通過一套算法利用計算機算出來。如何區分某個問題的“正”“反”？這並沒有一個嚴格的標準，但是我們可以粗略地這樣理解：世間的事物或現象之間往往存在著一定的自然順序，如時間順序、空間順序、因果順序，等等。所謂正問題，一般是按著這種自然順序來研究事物的演化過程或分布形態，起著由因推果的作用。反問題則是根據事物的演化結果，由可觀測的現象來探求事物的內部規律或所受的外部影響，由表及里，索隱探秘，起著倒果求因的作用。可以看出，正、反兩方面都是科學研究的重要內容。

基本介紹

• 中文名：數學物理反問題
• 外文名：Inverse problem of Mathematical Physics
• 適用領域：數學與物理的基本邏輯推理
• 所屬學科：自然科學

反問題介紹

儘管一些經典反問題的研究可以追溯很早，反問題這一學科的興起卻是近幾十年來的事情。在科學研究中經常要通過間接觀測來探求位於不可達、不可觸之處的物質的變化規律；生產中經常要根據特定的功能對產品進行設計，或按照某種目的對流程進行控制。這些都可以提出為某種形式的反問題。可見，反問題的產生是科學研究不斷深化和工程技術迅猛發展的結果，而計算技術的革命又為它提供了重要的物質基礎。

現在，反問題的研究已經遍及現代化生產、生活、研究的各個領域。簡單的概括不足以說明問題，我們下面具體介紹一些常見的反問題類型，希望大家能夠對它有一個概括的了解

定向設計

工業生產離不開產品設計，如何設計出優質產品使之更好地實現其功能，是關係到廠家信譽和企業生存的大問題。在這方面，從事反問題研究的數學家可以為企業家出謀劃策。

事實上，最早的反問題研究就是起源於定向設計問題。我們知道，單擺的等時性只是在小角度的假設下才近似成立。能不能找到一種特殊軌線的擺，使它嚴格滿足等時性？Huygens於1673年提出並解決了這一問題，這種特殊的軌線就是旋輪線，它的方程為到了十九世紀，挪威數學家Abel將Huygens的問題推廣為：測出了物體從不同高處落下的時間，如何反求物體下落的軌道？他於1823年給出了問題的解答。

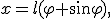
數學物理反問題

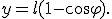
數學物理反問題

當代工業產品的極大豐富為反問題的研究提供了廣闊的用武之地，許多工業設計問題是相當困難的，需要用到高深的數學手段。例如，國外的光學儀器廠家提出：能否設計一種光柵，利用其非線性衍射效應產生出高能量的單色光射線？這就是一個定向設計問題，它要求數學家利用推導和計算手段構造出所需要的曲面（光柵）形狀。

定向設計不限於產品，它的套用相當廣泛。比如說：一個城市的某條街道車流量很大，不堪負荷，怎樣通過鋪設新的路段來進行分流？在軍事行動中如何對不同種類的炮火進行分布以達到特定的轟炸效果？這類問題往往涉及各種事物的組合、分配、布局，要求在各種相互制約、相互影響的因素中尋找出最佳方案，為領導的決策提供依據。

物性探測

給你一隻管子，不允許直接進入內部測量，你能算出裡面的形狀嗎？如果管子是軸對稱的，這時只需要知道內部的截面半徑就可以了。美國貝爾電話實驗室的Sondhi和Gophinath提供了一個方法：在管子的一邊發出聲音，用儀器測量管口的位移速度和壓力。通過測量結果就可以推知管內的截面半徑。理論計算與實驗結果吻合得很好。

不要小看了這個例子，它實際上暗示了許多不能直接測量的物性探測問題可以通過類似的間接方法來解決。我們通常說“上天入地”都是很困難的事情，可是在一些情況下似乎必須“入地”才能解決問題，比如說石油勘探。石油通常埋在幾千米的地下，無法直接觀察油田的位置和儲量，靠試打井的辦法來探測不但費用昂貴（一口井的代價要上千萬元），而且效率極低（只能探測到井附近的局部信息）。一個可行的辦法是通過地面爆炸向地下發射地震波，同時接收地層的反射波信號。可以想像，地面接收到的反射信號中含有地下的物性結構信息（地層的密度、聲速等等），利用數學手段將這些信息提取出來，就可以對地下的油儲及其分布作出科學的判斷。這很象在夏天人們挑西瓜，把瓜放在耳邊拍一拍，有經驗的人就知道瓜瓤熟不熟，不需要切開來看，不會破壞西瓜的完整。

類似的探測方法可以套用於許多方面，如：農用土壤分析、地下水勘查，甚至於在考古發現上也有套用。位於三峽庫區的四川省雲陽縣故陵鎮有一個大土包，相傳為楚國古墓，但是歷經三千餘年的變遷，已經難以確認了。科技工作者在地表利用地震波法、高精度磁法、電場岩性探測和地化方法四種手段進行探測，不但確認了古墓的存在，而且得到了關於古墓的埋藏深度、形狀、大小甚至墓道的準確信息，為搶救和保護文物作出了貢獻。

掃描成像

在前面講到的Abel反問題中，如果把下落的物體用掃描射線替代，從另一個角度來看它為我們提供了從射線的走時回響反推其傳播軌跡的方法，將不同軌跡射線的反演結果組合起來就能得到傳播介質的內部形態信息。本世紀初，Hebglotz和Wiechebt套用Abel型反演方法解決了在一定對稱條件下通過地震波的走時曲線來反推地層內部形貌的方法。據此Mohobovic（1909年）發現了地殼與地幔之間的斷層。現在，利用地震波的接收信號通過成像來考察地層地貌形態已經成為地球物理勘探最為重要的手段。例如，通過走時成像，可以得到地震波在不同深度的傳播速度；而在已知速度的前提下，利用聲波方程或其單程波方程偏移成像方法，又可以得到反射界面的位置和形狀。

成像的另一個重要套用是醫學上的計算機層析成像（CT），這是X光射線自Roentgen發明（獲1900年諾貝爾獎）以來在醫療診斷上的重大進展，其發明人Hounsfield和Cormack因此獲得了1979年的諾貝爾醫學獎。CT技術是醫學、電子技術、計算機技術和反演數學相結合的產物，它利用計算機來對穿越人體的X射線信號進行處理，來重建體內的結構信息，生成透視圖象供醫療診斷參考，其核心算法的數學基礎是二維Radon變換。繼之而起的是基於三維Radon變換的核磁共振成像，在診斷效果和無傷害性方面更為優越。事實上，類似的方法也可以藉助於聲波、光波、電磁波在無損探傷、雷達偵察、射電望遠鏡探測、環境監測等多方面有廣泛套用。

逆時反演及其它

在科學研究中，我們經常遇到這樣的問題：知道了某個事物的現在狀態，希望了解它的過去，即通常所說的“恢復歷史的本來面目。”這往往可以提為逆時反問題。當然，反問題研究不是歷史學，它所研究的對象一般要滿足某種類型的演化方程或數學模式。例如，通過遠程測得的某次爆炸產生的輻射波，如何確定爆炸的位置和初始能量？這是波動方程的逆時反問題；又如，根據近來的溫度變化能否確定過去某個時間的溫度狀態？這就成為熱傳導方程的逆時反問題。

前面介紹了反問題的幾種類型，它們在研究和套用上經常是相互聯繫的，分門別類只是為了敘述方便。另外，反問題與其它數學學科之間並沒有一個嚴格的界限，而是互為補充，互相促進。反問題的研究起源於數理方程，其反演算法中包含了微分方程數值解法、最最佳化方法和機率統計等方面的許多思想和技巧。另一方面，反問題的研究也促進了人們對世界的認識，使得研究更全面、深化。一個著名的例子是反散射方法在孤立子發現中的作用：反散射問題是量子物理學研究中的一個問題，通過譜和譜函式在無窮遠處的散射性態反推一維Schordinger方程的位勢函式。它由前蘇聯數學家Gelfand和Levitan（1955年）一舉解決。在此基礎上引發了一系列突破性進展，最為著名的是利用這個結果Lax（1968年）得到了關於KDV方程的巧妙解法，從而發現了非線性方程中的孤立子現象。這是近代非線性科學研究的重要事件。

反問題研究的難點及對策

與正問題相比，反問題的研究起步較晚，發展還遠不成熟。從本質上來說，反問題的研究的難度一般比相應的正問題要大。這是因為反問題的求解往往違背了物理過程的自然順序，從而使正問題中的許多良好性質不再滿足。這種現象在許多學科的研究中都是普遍存在的。比如說：曹雪芹創作了古典名著《紅樓夢》，這是人所共知的，但是要從現存的史料和文物“碎片”來恢復這位偉大作家的人生經歷和創作歷程則是一件萬分艱辛的事情，更何況這些“碎片”信息真偽交雜，且時有含混。反問題的研究也經常遇到類似的困難，這些困難體現在：

1. 存在性：我們要求的反問題的解很可能不存在。無解的原因多種多樣，可能是在定向設計中問題的提法不合理，也可能是探測時接收到的回響中含有假信息（噪音），將求解引入歧途。

2. 唯一性：有的反問題的解雖然存在，卻不唯一，有幾個甚至無窮多個。這是因為收集到的信息不夠，不足以確定解的性態。對大多數反問題（比如探測問題）來說，真正的解只有一個，這就要從許多解當中進行挑選，去偽存真，頗費周折。

3. 穩定性：利用計算手段，由接收信息來反演物質的結構和特性是反問題研究的重要內容。可是實際的接收回響中不可避免地含有噪音，計算過程也有累積誤差。這種微小的誤差會不會導致反演結果面目全非？研究表明，相當多的反問題正是具有這樣的病態性質！熱傳導方程的逆時反問題就是一個例子。熱力學第二定律告訴我們，熱傳導是一個不可逆過程，它的反問題求解是高度病態的。為了解決溫度的逆時反演，就不得不冒這種“差之毫厘，謬以千里”的危險。

存在性、唯一性和穩定性，三者之一不滿足就稱為不適定性問題。用傳統的眼光來看，這樣的問題是不值得研究的。正是反問題的研究開闊了人們的視野，認識到這樣的問題是大量存在的，而且有著重要的研究和套用價值。

如果一個問題的解不存在、不唯一、不穩定，那么求解得到的結果可信嗎？這是反演工作者必須面對的問題。解決的辦法是有的！奠基性工作是由前蘇聯Tikonov等學者提出的解決線性不適定問題的正則化方法。方法的主要思想是：利用對解和數據誤差的先驗估計可以將問題的求解限定在某個較小範圍內，對問題的提法進行適當的改造後，原本不適定的問題就可以轉化為適定的最最佳化問題求解，而且先驗估計表明在一定精度下用正則化方法求得的解是合理的。這比如猜謎：“後，打一人名”，無從猜起。如果限定“打《紅樓夢》中一人名”，範圍縮小了，可以用書中601個人物（有的書中沒有交代姓名）逐一比較，最後選出最優的答案－“王夫人”。

充分利用各種合理的先驗信息對問題作適當形式的轉換，是反問題求解的重要方法，在實際生產中經常要用到。拿地震波勘探為例，限於技術原因，地面接收的信號噪音很大，信息殘缺不全，完全的反演是很困難的。為了滿足生產的要求，必須盡最大可能恢復出地下的結構形態。這時，多種反演方法並用是一個可行的辦法；如果在目的地有一口油井，那么可以把井下的信息作為局部約束來校正反演結果；為了計算的穩定性還必須使用一些特殊的數學技巧。這樣得到的反演結果與資料解釋人員的經驗結合起來，可以對油田的決策與發展提供參考依據。

除了前面提到的不適定性以外，反問題的研究與套用還經常面臨非線性的困擾。即使正問題是線性的，它的反問題也往往表現為非線性，這為反演的研究和計算帶來了很多麻煩。為了求解非線性反問題，通常要線性化後反覆進行正、反演疊代，在高維情況下將導致十分巨大的計算量。我們知道，一個效率低下的算法在生產套用中將導致時間和人力、物力的極大浪費。所以反問題的計算效率也是一個非常重要的課題。它要求計算數學工作者從實際套用出發，充分研究問題的性質和特點，構造出精巧、快速的算法以適應生產的需要。

反演問題有著特殊的困難，它向我們提出了許多在認識論、方法論中富有挑戰

性的課題，深化了對客觀現象的理解。反問題的研究確有它獨立的價值。

發展和展望

反問題研究的興起不過是近幾十年的事情，它主要的研究對象是涉及與探測、識別和設計有關的套用問題。實際生產的迫切需求是推動這一學科迅速發展的原動力。1987年，以“反問題、反演方法和數據反演計算”為主要內容的專題雜誌Inverse Problems創刊，標誌著反問題的研究走向獨立和成熟。世界上每年都舉行各種形式的反問題研討會，得到了數學、物理、工程技術等多方面專家的回響。需要指出的是，在國外對反問題研究的資助不僅來自於科研和工業部門，還得到了國防部門的有力支持。

我國的反問題研究自八十年代初由馮康先生首倡，在實際問題的推動下，先後在中國科學院、哈爾濱工業大學、山東大學、中山大學、南京大學以及石油等工業部門多家單位取得相當數量的理論和實際套用成果。

近四十年來計算技術的飛速發展大大增強了數學工作者在自然科學、社會科學和工程技術等廣闊領域的參與能力，反問題正是在這樣的背景下應運而生的交叉性學科。它的生命力源於實際套用的迫切需求和反演工作者卓有成效的工作。反問題的出現為傳統數理方程的研究開闢了新的疆域，也為數學家參與實際生活提供了新的切入點。應該看到，反問題的開展程度與工業和國防的現代化、科學技術在產品中的含量有著密切的關係。我們期待著這一新興學科在國內能夠健康地發展起來，為國家的經濟建設作出它應有的貢獻。

發展狀況

近二十年來,數學物理反問題已成為套用數學中發展和成長最快的領域之一。之所以如此,在很大程度上是受其它學科與眾多工程技術領域的套用中產生的迫切需要所驅動；同時,由於它在理論上又具有鮮明的新穎性和挑戰性，所以引起了國內外許多學者和實際工作者從事研究和套用。迄今,它已發展成為具有交叉性的計算數學、套用數學和系統科學中的一個熱門學科方向。

分類

數學物理反問題的研究可分為研究和實際套用兩個方面，地質工程、醫學、軍事、環境、遙測、控制、通訊、氣象、經濟、管理等領域著重實際的套用；而數學研究著重研究問題的理論和方法。數學物理反問題是和數學物理正問題相對應的，我們稱一個先前研究的相對充分或完備的問題為正問題，它描述的是時空域中順時針的物理變化過程，一般是按某物理規律由因而果，由過去、現在來預測未來；而反問題描述的是時空域逆時針的物理變化過程，由果探求因。反問題又和問題的不適定性緊密聯繫在一起的，由於不適定問題大量的普遍存在，必然要求尋求合適的特殊的方法處理才能得到穩定的近似解各種反問題不勝枚舉，從實際套用角度來看，可以概括的說，有兩種不同的動機驅動著反問題的研究： （1）想了解物理過程過去的狀態或辯識其參數（以便為預測的目的服務）；（2）想了解如何通過干預當前的狀態或調整某些參數去影響（或控制）該系統，以便使其在未來達到人們所預期的狀態。因此我們可以這么說,反問題就是要定量的探求：在已觀察到的效果（表現）的背後的動因究竟是什麼?以及對於期望達到的效果而言，應當預先施加何種措施或控制？

求解方法

求解數學物理反問題所面臨的兩個本質性的實際問題是：(1)原始數據可能不屬於所論問題精確解所對應的數據集合，因而在經典意義下的近似解可能不存在；(2)近似解的不穩定性，即原始數據小的誤差會導致近似解與真解的嚴重偏離。總之，反問題常常是不適定的，是和不適定性緊密聯繫在一起的，若不採用特殊的方法求解，將得不到合理的答案。

一般地，反問題都是非線性的和不適定的，因而比求解正問題更困難。

套用領域

在遙測和勘探技術中提出了大量的反問題。例如，在地球物理勘探中，通過地震波的測量來判斷地球內部的結構或地下礦藏的位置;在無損探傷中,用紅外線掃描來探測固體材料中的缺陷；通過測量地面上的牛頓引力勢來推斷地下金屬礦藏的位置、形狀和密度;利用X光分層掃描構像來作醫學診斷等等，都是在研究對象不能達到或直接接觸的情況下，利用特定的物理手段來取得有關解的某些信息，而化為數學上的反問題來處理的。工程技術中的定向設計及系統識別等方面的問題，都屬於反問題的範疇。在量子物理中，利用散射資料來反推位勢的反散射問題，也是一類有重要意義的反問題。

反問題的提法多種多樣，且往往在經典的意義下是不適定的。為了求解各種不同形式的反問題，人們已經提出了一些有效的方法，如拉東變換、反散射方法、最優設計方法以及各種正則化方法等，但是還有很多問題有待進一步的研究。