三門問題(Monty Hall problem)亦稱為蒙提霍爾問題、蒙特霍問題或蒙提霍爾悖論,大致出自美國的電視遊戲節目Let's Make a Deal。問題名字來自該節目的主持人蒙提·霍爾(Monty Hall)。參賽者會看見三扇關閉了的門,其中一扇的後面有一輛汽車,選中後面有車的那扇門可贏得該汽車,另外兩扇門後面則各藏有一隻山羊。當參賽者選定了一扇門,但未去開啟它的時候,節目主持人開啟剩下兩扇門的其中一扇,露出其中一隻山羊。主持人其後會問參賽者要不要換另一扇仍然關上的門。問題是:換另一扇門會否增加參賽者贏得汽車的機率?如果嚴格按照上述的條件,即主持人清楚地知道,自己打開的那扇門後是羊,那么答案是會。不換門的話,贏得汽車的幾率是1/3。換門的話,贏得汽車的幾率是2/3。
這個問題亦被叫做蒙提霍爾悖論:雖然該問題的答案在邏輯上並不自相矛盾,但十分違反直覺。這問題曾引起一陣熱烈的討論。
基本介紹
- 中文名:三門問題
- 外文名:Monty Hall problem
- 別稱:蒙提霍爾問題
- 提出者:蒙提霍爾
問題,由來,假設,解答,解法一,解法二,補充說明,迴響,相關討論,相關影片,
問題
由來
以下是蒙提霍爾問題的一個著名的敘述,來自 Craig F. Whitaker 於1990年寄給《展示雜誌》(Parade Magazine)瑪麗蓮·沃斯·莎凡特(Marilyn vos Savant)專欄的信件:
“假設你正在參加一個遊戲節目,你被要求在三扇門中選擇一扇:其中一扇後面有一輛車;其餘兩扇後面則是山羊。你選擇了一道門,假設是一號門,然後知道門後面有什麼的主持人,開啟了另一扇後面有山羊的門,假設是三號門。他然後問你:“你想選擇二號門嗎?”轉換你的選擇對你來說是一種優勢嗎?”
以上敘述是對Steve Selvin於1975年2月寄給American Statistician雜誌的敘述的改編版本。如上文所述,蒙提霍爾問題是遊戲節目環節的一個引申;蒙提·霍爾在節目中的確會開啟一扇錯誤的門,以增加刺激感,但不會容許參賽者更改他們的選擇。如蒙提·霍爾寄給Selvin的信中所寫:
“如果你上過我的節目的話,你會覺得遊戲很快—選定以後就沒有交換的機會。”
Selvin在隨後寄給American Statistician的信件中(1975年8月)首次使用了“蒙提霍爾問題”這個名稱。
一個實質上完全相同的問題於1959年以“三囚犯問題”(three prisoners problem)的形式出現在馬丁·加德納(Martin Gardner)的《數學遊戲》專欄中。加德納版本的選擇過程敘述得十分明確,避免了《展示雜誌》版本里隱含的前提條件。
這條問題的首次出現,可能是在1889年約瑟夫·貝特朗所著的 Calcul des probabilités 一書中。 在這本書中,這條問題被稱為“貝特朗箱子悖論”(Bertrand's Box Paradox)。
假設
Mueser 和 Granberg 透過釐清細節,以及對主持人的行為加上明確的介定,提出了對這個問題的一種不含糊的陳述︰
- 現在有三扇門,只有一扇門有汽車,其餘兩扇門的都是山羊。
- 汽車事前是等可能地被放置於三扇門的其中一扇後面。
- 參賽者在三扇門中挑選一扇。他在挑選前並不知道任意一扇門後面是什麽。
- 主持人知道每扇門後面有什麼。
- 如果參賽者挑了一扇有山羊的門,主持人必須挑另一扇有山羊的門。
- 如果參賽者挑了一扇有汽車的門,主持人等可能地在另外兩扇有山羊的門中挑一扇門。
- 參賽者會被問是否保持他的原來選擇,還是轉而選擇剩下的那一扇門。
轉換選擇可以增加參賽者拿到汽車的機會嗎?
解答
解法一
問題的答案是可以:當參賽者轉向另一扇門而不是維持原先的選擇時,贏得汽車的機會將會加倍。
有三種可能的情況,全部都有相等的可能性(1/3):
參賽者挑山羊一號,主持人挑山羊二號。轉換將贏得汽車。
參賽者挑山羊二號,主持人挑山羊一號。轉換將贏得汽車。
“參賽者挑汽車,主持人挑羊一號。轉換將失敗”,和“參賽者挑汽車,主持人挑羊二號。轉換將失敗。”此情況的可能性為: 。
。

解法二
另一種解答是假設你永遠都會轉換選擇,這時贏的唯一可能性就是選一扇沒有車的門,因為主持人其後必定會開啟另外一扇有山羊的門,消除了轉換選擇後選到另外一隻羊的可能性。因為門的總數是三扇,有山羊的門的總數是兩扇,所以轉換選擇而贏得汽車的機率是2/3,與初次選擇時選中有山羊的門的機率一樣。
補充說明
第一次選的空門(機率66.6%),之後主持人開另一個空門,換門,得到汽車。
第一次選的汽車(機率33.3%),之後主持人開另一個空門,不換門,得到汽車。
這裡影響到結果的機率問題只發生在第一次選門上,如果條件如上設定,當一開始的門選定後,事件的結果也就決定了,所以這裡不存在之後主持人是選擇1號空門,還是2號空門的問題,所以在做機率計算是不考慮主持人的選擇。如果也要考慮主持人的話:
第一次選的空門1(機率1/3),之後主持人開另一個空門,換門,得到汽車。事件總機率1/3。
第一次選的空門2(機率1/3),之後主持人開另一個空門,換門,得到汽車。事件總機率1/3。
第一次選的汽車(機率1/3),之後主持人開另一個空門1(機率1/2),不換門,得到汽車 這個事件總機率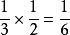 。
。
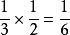
第一次選的汽車(機率1/3),之後主持人開另一個空門2(機率1/2),不換門,得到汽車 這個事件總機率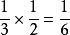 。
。
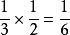
主持人選1號空門還是2號空門打開,這裡有個主持人的選擇機率,我假設的是主持人隨機選擇(抽籤或者隨意),所以各給了50%的機率,如果主持人就是喜歡1號空門,必開1號,那么也就成了1號(100%),2號(0%)了,最後結果並不影響。
所以開始選中汽車,最後換門不得獎的機率是33.3%,開始選中空門,換門最後得獎的機率是66.6%。
迴響
對於“蒙提霍爾問題”(“Monty Hall dilemma”),瑪麗蓮·沃斯·莎凡特在她專欄的回答是改選會更有優勢,這在美國引起了激烈的爭議:人們寄來了數千封抱怨信,很多寄信人是科學老師或學者。一位來自佛羅里達大學的讀者寫道:“這個國家已經有夠多的數學文盲了,我們不想再有個世界上智商最高的人來充數!真讓人羞愧!”另一個人寫道:“我看你就是那隻山羊!”美國陸軍研究所(US Army Research Institute)的埃弗雷特·哈曼(Everett Harman)寫道,“如果連博士都要出錯,我看這個國家馬上要陷入嚴重的麻煩了。”
但是莎凡特並沒有錯。最後她用整整4個專欄,數百個新聞故事及在小學生課堂模擬的測驗來說服她的讀者她是正確的。“喔,那真是太有趣了。實際上我十分享受這些討厭的來信,”她說。“這些傢伙我真是愛死他們了!”
這一問題的關鍵在於主持人,因為他總會挑一扇後面沒有獎品(汽車)的門。遊戲秀的調查數據顯示,那些改選的參賽選手贏的幾率是那些沒有改選的人的兩倍,這證實了莎凡特在其第三篇專欄中的解釋:“當你從三扇門中選了門1後,這扇門後面有獎的幾率是1/3,另兩扇門是2/3。但接下來主持人給了你一個線索。如果獎品在門2後,主持人將會打開門3;如果獎品在門3後,他會打開門2。所以如果你改選的話,只要獎品在門2或門3後你就會贏,兩種情況你都會贏!但是如果你不改選,只有當獎品在門1後你才會贏。"
總結一句話,機率存在於被給予的條件下,機率不能寄托在實際的物體上
相關討論
流言終結者(Mythbusters)是美國的科普電視節目,它也在2011年11月做了一次關於三門問題的實驗。
相關影片
《決勝21點》

