整數矩陣(integer matrix)是在數論中有重要套用的一種矩陣,指元素aij(i,j=1,2,…,n)都是整數的n階矩陣A=(aij),若n階整數矩陣A的行列式|A|=±1,則A稱為麼模整數矩陣,一個整數矩陣有逆整數矩陣,若且唯若這個矩陣是麼模整數矩陣。
基本介紹
- 中文名:整數矩陣
- 外文名:integer matrix
- 所屬學科:數學
- 所屬問題:數論(矩陣)
- 簡介:元素都是整數的n階矩陣
定義

相關概念及性質










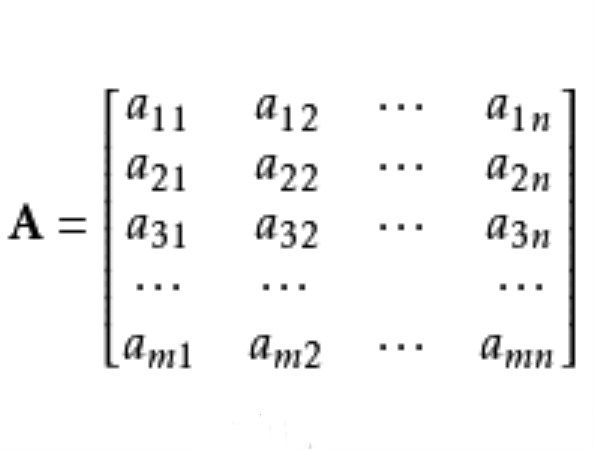
整數矩陣(integer matrix)是在數論中有重要套用的一種矩陣,指元素aij(i,j=1,2,…,n)都是整數的n階矩陣A=(aij),若n階整數矩陣A的行列式|A|=±1,則A稱為麼模整數矩陣,一個整數矩陣有逆整數矩陣,若且唯若這個矩陣是麼模整數矩陣。











整數矩陣(integer matrix)是在數論中有重要套用的一種矩陣,指元素aij(i,j=1,2,…,n)都是整數的n階矩陣A=(aij),若n階整數矩陣A的行列式|A|=±1,則A稱為麼模整數矩陣,一個整數矩陣有逆...
關於整數線性規劃問題 網路最最佳化的許多問題常常可以用一個整數線性規劃模型來描述。整數線性規劃是指要求變數取整數值的線性規劃。考慮整數線性規劃問題 這裡,“ ”是指 的每個分量都是非負整數。所有元素均是整數的矩陣稱為整數矩陣。
仍然是埃爾米特矩陣。如果A是埃爾米特矩陣,對於正整數n, 是埃爾米特矩陣。方陣C與其共軛轉置的和是埃爾米特矩陣。任意方陣C都可以用一個埃爾米特矩陣A與一個斜埃爾米特矩陣B的和表示。埃爾米特矩陣是正規矩陣,因此埃爾米特矩陣可被酉...
魔方矩陣又稱幻方,是有相同的行數和列數,並在每行每列、對角線上的和都相等的矩陣。魔方矩陣中的每個元素不能相同。你能構造任何大小(除了2x2)的魔方矩陣。基本介紹 在《射鵰》中郭黃二人被裘千仞追到黑龍潭,躲進瑛姑的小屋。
費馬矩陣:當整數n >2時,如果有m階矩陣A ,B ,C ,且aij∈N ,bij∈N ,cij∈N ;則對於矩陣方程 A^n + B^n =C^n是否有正整數的矩陣解。顯然,費馬大定理只是m=1的特殊情況。費馬大定理簡介 費馬大定理:當整數n ...
在數學中,嘉當矩陣是由法國數學家埃利·嘉當引入的一類特別矩陣,最大的套用在於李代數的分類理論。在有限維代數的表示理論中,嘉當矩陣另有其它意義。李代數 所謂廣義嘉當矩陣是具有下述性質的方陣 :各項皆為整數:。對角線上的項等於...
矩陣函式的概念與通常的函式概念類似,不同在於矩陣函式的自變數和因變數都是n階矩陣。矩陣函式一般用冪級數表示。矩陣函式與矩陣值函式是矩陣理論的重要內容,它們在力學、控制理論、信號處理等學科中具有重要套用。定義 設復變冪級數 的...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。線上性代數中,對於n階方陣N,存在正整數k,使得N^k=0,這樣的方陣N就叫做冪...
若A和B是埃爾米特矩陣,那么它們的和A+B也是埃爾米特矩陣;而只有在A和B滿足交換性(即AB=BA)時,它們的積才是埃爾米特矩陣。可逆的埃爾米特矩陣A的逆矩陣 仍然是埃爾米特矩陣。如果A是埃爾米特矩陣,對於正整數n, 是埃爾米特矩陣...
對稱C矩陣(symmetric conference matrix)是與阿達馬矩陣有關的一類矩陣。若元素為士1的n階對稱矩陣C的對角線元均為1且適合等式(C一1)2= 1,則稱C為對稱C矩陣.這類矩陣在研究會議電話系統時遇到,因而得名。這類矩陣可用於H矩陣...
是一個二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,如果兩者相等,則其輸出值為1,否則為0。克羅內克函式的值一般簡寫為 。克羅內克函式和狄拉克δ函式都使用δ作為符號,但是克羅內克...
稱重矩陣(weighing matrix)是阿達馬矩陣的推廣,若W是元素為0,±1的n階矩陣,且使WW=kIₙ,則稱W為n階稱重矩陣,k=n的稱重矩陣就是n階阿達馬矩陣,k=n-1的對稱稱重矩陣就是n階對稱C矩陣,人們猜測:對每個正整數t及每個k=...
冪么矩陣(unipotent matrix)一種特殊矩陣,指冪么變換所對應的矩陣。冪么矩陣(unipotent matrix)一種特殊矩陣.指冪么變換所對應的矩陣.即存在正整數m,使A'"=E的n階矩陣A.冪么矩陣A是可逆的,且其逆矩陣為A’一‘;A的特徵值的...
需要說明的是,圖中各個部件的數目僅為示意性的,可以具有任意數目的數據匯流排和陣列處理機,陣列處理機202中的PE的數目為k個(k為大於1的整數),而不限於圖中所示的3個。數據匯流排201可以用於從存儲待執行矩陣乘運算的被乘數矩陣和乘數...
NumPy(Numerical Python)是Python的一種開源的數值計算擴展。這種工具可用來存儲和處理大型矩陣,比Python自身的嵌套列表(nested list structure)結構要高效的多(該結構也可以用來表示矩陣(matrix)),支持大量的維度數組與矩陣運算,此外...
埃爾米特形式(Hermite Normal form)是複流形上的一種特殊雙線性形式。基本簡介 線上性代數中,埃爾米特形式是整數Z上矩陣的簡化階梯形式的一個類似形式。就像簡化的階梯形式可以用來解決關於線性系統的解的問題Ax = b其中x在Rn中, ...
二維數組本質上是以數組作為數組元素的數組,即“數組的數組”,類型說明符 數組名[常量表達式][常量表達式]。二維數組又稱為矩陣,行列數相等的矩陣稱為方陣。對稱矩陣a[i][j] = a[j][i],對角矩陣:n階方陣主對角線外都是零...
幻方,有時又稱魔方(該稱呼現一般指立方體的魔術方塊)或縱橫圖,由一組排放在正方形中的整數組成,其每行、每列以及兩條對角線上的數之和均相等。通常幻方由從1到N²的連續整數組成,其中N為正方形的行或列的數目。因此 N階...
當行列式為0或近似於0時,其對應逆矩陣不存在,或雖然存在,但計算機計算出來的結果不正確。(2)語法:d = det(X)返回方陣X的行列式值。如果X僅包含一個整數元素,返回的結果d也是一個整數。(3)解析:將der(X)==0作為對矩陣奇異...
不變因子是λ-矩陣理論中的概念,λ矩陣 A (λ)最後化成的史密斯標準型,其對角線的元素d₁(λ),d₂(λ),...,dₐ(λ)稱為 A (λ)的不變因子。基本概念 設 是n階 一矩陣,k是小於等於n的某個正整數,如果 的...
整表示是一類特殊的線性表示。設R是一個整環,其分式域為F,若群G在域F上的一個矩陣表示使得對任g∊G,矩陣T(g)的每個元素均在R中,則稱這種表示為整表示。若R是一個主理想整環,其分式域為F,則每個F表示均等價於一個R...
