基本介紹
- 中文名:伴隨矩陣
- 外文名:Adjugate matrix
- 本質:類似於逆矩陣的概念
- 領域:線性代數
- 特點:與逆矩陣只差一個係數
- 性質:與原矩陣形成映射
定義
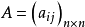
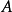



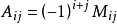

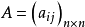
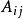
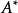

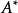
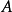
性質
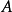
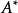
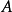

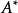
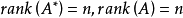
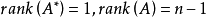
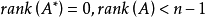
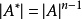
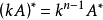
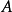
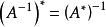
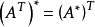
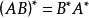
特殊求法
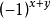

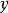

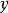

m重伴隨矩陣
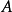
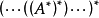
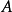
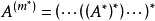
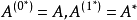
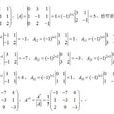
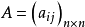
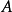



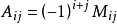

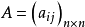
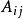
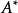

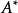
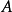
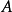
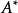
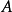

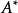
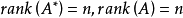
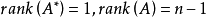
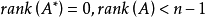
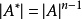
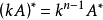
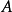
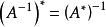
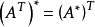
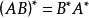
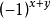

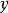

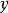

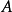
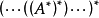
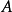
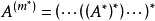
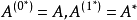
線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果二維矩陣可逆,那么它的逆矩陣和它的伴隨矩陣之間只差一個係數,對多維矩陣也存在這個規律。...
伴隨陣,又稱伴隨矩陣(adjoint matrix)。設R是一個交換環,A是一個以R中元素為係數的 n×n 的矩陣。A的伴隨矩陣可按如下步驟定義:定義1:A關於第i 行第j ...
經典伴隨變換(classical adjoint transformation)是向量空間中的一種線性變換。線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果矩陣可逆,那么它的...
數學上,特別是泛函分析中,希爾伯特空間中的每個線性運算元有一個相應的伴隨運算元(adjoint operator)。運算元的伴隨將方塊矩陣共軛轉置推廣到(可能)無窮維情形。如果我們將...
傳遞函式矩陣(transfer function matrix)表示線性定常控制系統輸入向量對狀態向量、輸入向量對輸出向量傳遞關係的矩陣。用於多輸入多輸出控制系統的分析研究。...
矩陣求逆,即求矩陣的逆矩陣。矩陣是線性代數的上要內容,很多實際問題用矩陣的思想去解既簡單又快捷。逆矩陣又是矩陣理論的很重要的內容,逆矩陣的求法自然也就...
代數式包括有理式(整式,分式)和無理式。線上性代數中用矩陣(向量)代替代數式中的實數,得到的代數式稱為矩陣代數式。矩陣代數式遵守代數式的規律,同時具備特殊...
矩陣行列式是指矩陣的全部元素構成的行列式,設A=(aij)是數域P上的一個n階矩陣,則所有A=(aij)中的元素組成的行列式稱為矩陣A的行列式,記為|A|或det(A)。若...
初等矩陣是指由單位矩陣經過一次三種矩陣初等變換得到的矩陣。初等矩陣的模樣可以寫一個3階或者4階的單位矩陣。首先:初等矩陣都可逆,其次,初等矩陣的逆矩陣其實是一...
整數矩陣(integer matrix)是在數論中有重要套用的一種矩陣,指元素aij(i,j=1,2,…,n)都是整數的n階矩陣A=(aij),若n階整數矩陣A的行列式|A|=±1,則A稱...
本書是根據蘇聯國立技術理論書籍出版社於1953年出版的甘特馬赫爾所著的《矩陣論》來譯出的,本書分上、下兩冊,上冊為原書第一部分:矩陣的理論基礎,包括第1至10...
《三維空間張量分析的矩陣方法》是2010年航空工業出版社出版的圖書,作者是李洲聖、唐長紅。本書採用非傳統方法討論張量的概念和運算。...
A的餘子矩陣是指將A的(i,j)代數餘子式擺在第i行第j列所得到的矩陣,記為C。C的轉置矩陣稱為A的伴隨矩陣,伴隨矩陣類似於逆矩陣,並且當A可逆時可以用來計算...
adj是一個線性代數術語。在矩陣理論中,adj表示一個矩陣的伴隨矩陣;線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果矩陣可逆,那么它的逆矩陣...
哈密頓-凱萊定理(Hamilton-Cayley theorem)是矩陣的一個重要性質,該定理表述為:設A是數域P上的n階矩陣,f(λ)=|λE-A|=λn+b1λn-1+…+bn-1λ+bn是A...
)。它在某個矩陣A處的展開為也就是說,在裝備正則範數的矩陣空間Mn()中,伴隨矩陣是行列式函式的梯度特別當A為單位矩陣時,可逆矩陣的可微性說明一般線性群GLn()...
上的矩陣 [2] 。凱萊-哈密頓定理可以視為線性代數中拉普拉斯展開的推論。拉普拉斯展開可推出若 是 矩陣,而 表其伴隨矩陣,則取 ,便得到 。此式對所有 皆成立,...
5.14其他各類矩陣的幾何意義 2045.14.1 逆矩陣的幾何意義 2045.14.2 轉置矩陣的幾何意義 2065.14.3 伴隨矩陣的幾何意義 213...
