基本介紹
- 中文名:哈密爾頓-凱萊定理
- 外文名:Cayley–Hamilton theorem
- 分類:數理科學
定義
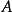
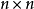
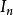
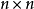

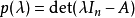
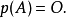
例子
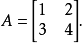
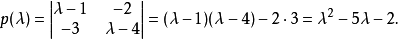
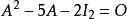

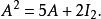
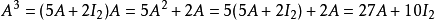

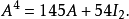


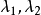
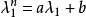
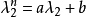

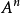
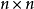


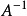

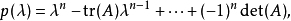
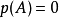
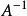

定理證明



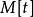

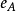
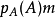
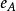

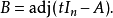
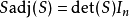



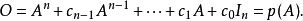
抽象化與推廣



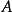
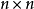
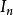
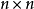

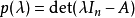
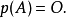
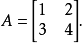
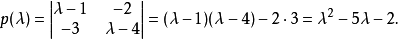
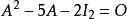

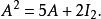
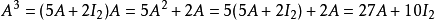

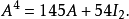


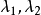
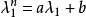
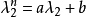

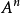
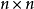


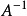

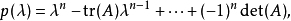
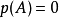
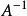




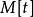

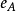
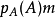
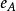

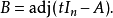
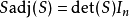



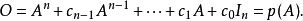



線上性代數中,凱萊-哈密頓定理(Cayley–Hamilton theorem)(以數學家阿瑟·凱萊與威廉·盧雲·哈密頓命名)表明每個布於任何交換環上的實或複方陣都滿足其特徵方程式...
在對複數長期研究的基礎上,他於1843年正式提出四元數這一概念,是代數學中的一項重要成果。此外,他還在矩陣理論中提出了哈密爾頓-凱萊定理。...
凱萊-哈密爾頓定理斷言任意矩陣A都是特徵方程的根:如果p是A的特徵多項式,那么p(A) = 0。這個定理一樣可以用若爾當標準型直接計算得出。...
數學上以凱萊命名的有:八元數,又稱Cayley數凱萊定理凱萊表凱萊圖凱萊公式凱萊-哈密爾頓定理Grassmann-凱萊代數詞條標籤: 科學家 圖集 阿瑟·凱萊圖冊 V百科往期回顧...
本書從一道高中數學聯賽試題的解法談起,詳細介紹了哈密爾頓-凱萊定理的相關知識。全書共分為五章,分別為:引言、基礎篇、套用篇、人物篇與進一步的討論。本書可供...
《高等代數典型問題精講:思想·方法·技巧》深入研究了矩陣的哈密爾頓-凱萊定理、矩陣的最小多項式、矩陣的相似理論、矩陣的有理標準、若爾當標準形、矩陣的滿秩分解...
本書深入研究了矩陣的哈密爾頓-凱萊定理、矩陣的最小多項式、λ矩陣、矩陣的相似理論、矩陣的有理標準、若爾當標準形、矩陣的滿秩分解、簡單的矩陣方程、矩陣乘積的...
根據哈密爾頓一凱萊定理,任意數域P上一個n階方陣A,其特徵多項式 是A的化零多項式,這一點保證了化零多項式的存在性。稱以A為根的次數最低且首項係數為1的...
凱利還提出了凱萊-哈密爾頓定理,並驗證了3×3矩陣的情況,又說進一步的證明是不必要的。哈密爾頓證明了4×4矩陣的情況,而一般情況下的證明是德國數學家弗羅貝尼烏斯...
第4章線性變換,討論線性變換的運算、線性變換的特徵值與特徵向量、可對角化的線性變換及哈密爾頓一凱萊定理。第5章歐幾里得空間,討論了歐氏空間的標準基、對稱變換、...
3.相似矩陣、相似不變數、哈密爾頓-凱萊定理. 4. 線性變換的值域與核、不變子空間. 若當標準形 1.矩陣. 2. 行列式因子、不變因子、初等因子、矩陣相似的條件...
鄭泉水通過連續幾天的冥思苦想,終於找到解答,後經整理聯名發表了《凱萊-哈密爾頓定理的兩個簡單證法和兩個表現定理》。後來,鄭泉水在楊德品、熊祝華、郭仲衡、黃克智...
6.3 凱萊一哈密爾頓定理 6.4 線性變換的特徵值和特徵向量 *6.5 套用:萊斯利模型 *6.6 最小多項式 *6.7 若當標準形簡介 第七章 正交性與最小二乘法 7.1...
《高等代數典型問題精講:思想·方法·技巧》是2009年科學出版社出版的圖書。本書深入研究了矩陣的哈密爾頓-凱萊定理、矩陣的最小多項式、矩陣的相似理論、矩陣的有理...
7.7.5 哈密爾頓一凱萊定理7.8 值域與核7.8.1 基本概念7.8.2 線性空間中線性變換的性質7.8.3 有關冪等變換的一些問題7.8.4 線性空間V到U的線性映射的...
