基本介紹
- 中文名:矩陣求逆
- 外文名:matrix inversion
- 學科:數學
- 釋義:求矩陣的逆矩陣
- 相關概念:逆矩陣
- 典型方法:利用定義求逆矩陣、初等變換法等
初等變換法






伴隨陣法

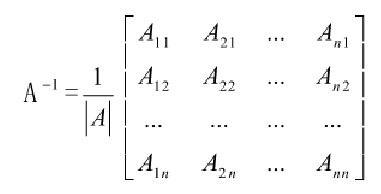





定義法和恆等變形法
利用定義求逆矩陣
恆等變形法
















矩陣求逆,即求矩陣的逆矩陣。矩陣是線性代數的上要內容,很多實際問題用矩陣的思想去解既簡單又快捷。逆矩陣又是矩陣理論的很重要的內容,逆矩陣的求法自然也就...
矩陣求逆法是求已知矩陣的逆矩陣的計算方法。...... 矩陣求逆法(numerical method ofinverseof amatrix)設矩陣的A的逆矩陣A一i-A -X一[ x xz,""",x },...
設A是數域上的一個n階矩陣,若在相同數域上存在另一個n階矩陣B,使得: AB=BA=E ,則我們稱B是A的逆矩陣,而A則被稱為可逆矩陣。注:E為單位矩陣。...
矩陣的逆和偽逆是數學領域中線性代數關於矩陣的名詞。...... 偽逆矩陣是逆矩陣的廣義形式。由於奇異矩陣或非方陣的矩陣不存在逆矩陣,但可以用函式pinv(A)求其偽...
列昂捷夫逆矩陣(Lconticf inversc matrix)投入產出模型中的一個重要數學概念。由*列昂捷夫首先提出,故稱。令X為各部門總產值列向量,I為單位矩陣,A為直接消耗係數...
求矩陣的群逆,A^#...... 求矩陣的群逆,A^# 設A∈ (r>0).若,A滿秩分解A=FG,且GF可逆,則矩陣A的群逆A^#=參考資料 1. 張凱院,徐仲.矩陣論:西北工...
根據反函式定理,一個可逆函式(存在反函式的函式)的雅可比矩陣的逆矩陣即為該函式的反函式的雅可比矩陣。即,若函式 在點 的雅可比矩陣是連續且可逆的,則F在點 p...
學科:核地質學 詞目:逆矩陣法 英文:inverse matrix method 釋文:逆矩陣法是γ測井分層解釋的一種方法。測量點的γ照射量率與單元層的鈾含量可以表示為一個線性...
分塊矩陣的初等變換是線性代數中重要而基本的運算,它在研究矩陣的行列式、特徵值、秩等各種性質及求矩陣的逆、解線性代數方程組中有著廣泛的套用 [1] 。...
對於矩陣方程,當係數矩陣是方陣時,先判斷是否可逆。如果可逆,則可以利用左乘或右乘逆矩陣的方法求未知矩陣,如果方陣不可逆或是係數矩陣不是方陣,則需要用矩陣的廣義...
希爾伯特矩陣是一種數學變換矩陣,正定,且高度病態(即,任何一個元素髮生一點變動,整個矩陣的行列式的值和逆矩陣都會發生巨大變化),病態程度和階數相關。...
1.3.3矩陣的秩 1.3.4常見錯誤 習題1.3 1.4逆矩陣 1.4.1逆矩陣的概念 1.4.2逆矩陣的求法 1.4.3逆矩陣的套用 1.4.4常見錯誤 習題1.4 複習...
這樣,可以通過對相機的變換矩陣求逆來得到模型的變換矩陣。下面來具體看一下,如何得到相機變換矩陣,並且求得它的逆矩陣。首先聲明一下,對於一個模型的變換,我們...
(2)從而得出旋轉矩陣的逆矩陣是它的轉置矩陣:這裡的 是單位矩陣。(3)一個矩陣是旋轉矩陣,若且唯若它是正交矩陣並且它的行列式是單位一。正交矩陣的行列式是 ±...
M矩陣是L矩陣的一種,M矩陣要求它自身的逆矩陣為一個非負矩陣。...... M矩陣是L矩陣的一種,M矩陣要求它自身的逆矩陣為一個非負矩陣。中文名 M矩陣 外文名 ...
稱為關係的求逆運算符。例如實數集合上的“大於等於”關係和“小於等於”關係。...根據關係代數和布爾矩陣代數的同構性質,有因此可得逆關係例題解析 編輯 ...
用矩陣表示線性變換的一個主要動力就是可以很容易地進行組合變換以及逆變換。 [2] 組合變換:組合可以通過矩陣乘法來完成。如果A與B是兩個線性變換,那么對向量x先...
全書共7章,內容包括:線性空間與線性變換,矩陣的變換和分解,矩陣範數及其套用,矩陣分析,特徵值的估計及對稱矩陣的極性,幾類特殊矩陣,矩陣的廣義逆與直積及其套用。...
