行列式的階越低越容易計算,於是很自然地提出,能否把高階行列式轉換為低階行列式來計算,為此,引入了餘子式和代數餘子式的概念。
在n階行列式中,把所在的第i行與第j列划去後,所留下來的n-1階行列式叫元的餘子式。
基本介紹
- 中文名:餘子式
- 外文名:cofactor
- 學科:數理科學
- 特點:行列式的一種
- 相關術語:代數餘子式
- 套用:線性代數、矩陣論
行列式餘子式
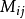
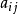
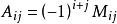


矩陣餘子式
其他相關定義
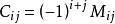

行列式的階越低越容易計算,於是很自然地提出,能否把高階行列式轉換為低階行列式來計算,為此,引入了餘子式和代數餘子式的概念。
在n階行列式中,把所在的第i行與第j列划去後,所留下來的n-1階行列式叫元的餘子式。
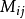
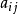
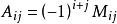
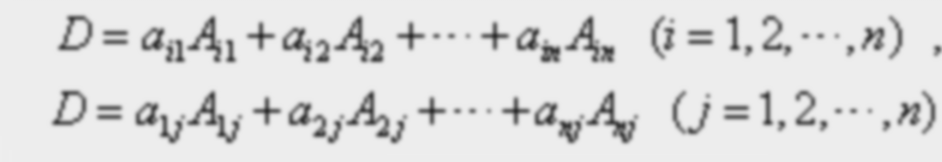


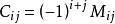
行列式的階越低越容易計算,於是很自然地提出,能否把高階行列式轉換為低階行列式來計算,為此,引入了餘子式和代數餘子式的概念。在n階行列式中,把所在的第i行與...
在n階行列式中,把元素aₒₑi所在的第o行和第e列划去後,留下來的n-1階行列式叫做元素aₒₑi的餘子式,記作Mₒₑ,將餘子式Mₒₑ再乘以-1的...
1 定義 2 子式和餘子式 主子式定義 編輯 在n 階行列式中,選取行號(如 1、3、7行),再選取相同行號的列號(1、3、7 列),則有行和列都為i個的行列式即...
套用梅森公式將大大簡化結構變換的計算,但當系統結構比較複雜時,很容易判斷錯誤前向通道、迴路、餘子式的數目,因此常常將梅森公式和結構圖變換結合起來用。也經常用...
行列式某元素的代數餘子式:行列式某元素的餘子式與該元素對應的正負符號的乘積.三階行列式運算 即行列式可以按某一行或某一列展開成元素與其對應的代數餘子式的乘...
方陣 的各元素的代數餘子式 所構成的如下矩陣 : 該矩陣 稱為矩陣A的伴隨矩陣。 性質 伴隨矩陣是矩陣理論及線性代數中的一個基本概念,是許多數學分支研究的重要...
將一個n×n矩陣B的行列式進行拉普拉斯展開,即是將其表示成關於矩陣B的某一行(或某一列)的n個元素的(n-1)×(n-1)餘子式的和。 [1] ...
也就是說, A的伴隨矩陣是一個n×n的矩陣(記作adj(A)),使得其第i 行第j 列的元素是A關於第j 行第i 列的代數餘子式。 [1] 中文...
一個n階的行列式M可以寫成一行(或一列)的元素與對應的代數餘子式的乘積之和,叫作行列式按一行(或一列)的展開。這個公式又稱拉普拉斯公式,把n維矩陣的行列式計算...
,Anj分別為它們在D中的代數餘子式,則D=a1jA1j+a2jA2j+…+anjAnj稱為行列式D的依列展開。例如,在一個三階行列式D中,划去元素aij(i=1, 2,3; j=1, ...
定義:A關於第i 行第j 列的餘子式(記作Mij)是去掉A的第i行第j列之後得到的(n − 1)×(n − 1)矩陣的行列式。 定義:A關於第i 行第j 列的代數余...
,Ain分別為它們在D中的代數餘子式,則D=ai1Ai1+ai2Ai2+…+ainAin稱為行列式D的依行展開。如果行列式D的第i行各元素與第j行各元素的代數餘子式對應相乘後...
4.n階行列式中任意一行(列)的所有元素與另一行(列)的相應元素的代數餘子式的乘積之和等於零。即當 時有由性質3和性質4,可得到如下結論:...
【第3條】代數餘子式計算口訣:奇負偶正(當行標與列標之和為奇數時,代數餘子式等於負的餘子式即餘子式的相反數;當行標與列標之和為偶數時,代數餘子式...
