不變因子是λ-矩陣理論中的概念,λ矩陣A(λ)最後化成的史密斯標準型,其對角線的元素d1(λ),d2(λ),...,da(λ)稱為A(λ)的不變因子。
基本介紹
- 中文名:不變因子
- 外文名:invariant factor
- 所屬學科:數理科學
- 相關概念:行列式因子
基本概念




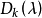





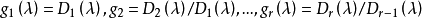

相關定理
定理1

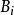
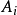

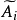
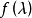
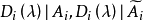

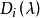
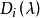
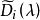
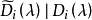
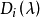

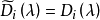
推論1
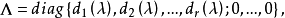
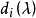
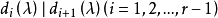
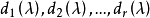
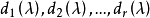
推論2
推論3
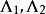
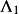
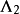

定理2

推論4
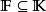

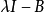
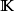
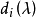
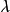
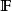
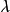
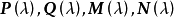
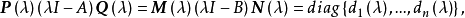
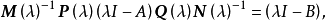

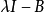
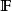
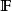

不變因子是λ-矩陣理論中的概念,λ矩陣A(λ)最後化成的史密斯標準型,其對角線的元素d1(λ),d2(λ),...,da(λ)稱為A(λ)的不變因子。




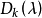





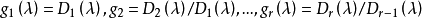


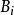
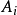

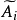
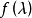
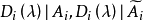

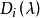
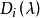
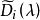
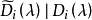
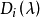

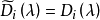
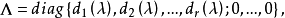
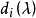
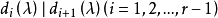
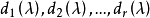
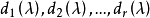
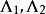
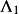
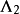



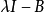
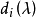
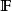
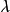
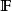
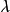
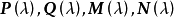
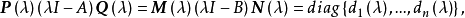
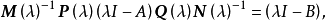

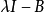
不變因子是λ-矩陣理論中的概念,λ矩陣A(λ)最後化成的史密斯標準型,其對角線的元素d₁(λ),d₂(λ),...,dₐ(λ)稱為A(λ)的不變因子。...
互動因子(Interaction factor)亦稱互動因素、共變因子(素)。析因試驗中,把因子間的互動效應構想為某一“因子”的作用,並稱之為“互動因子”。互動效應客觀是存在...
設A是n級複數矩陣,則A的最小多項式 是A的最後一個不變因子 。[2] 最小多項式例題 求 的最小多項式。[3] 解:A的特徵多項式為:...
的k階行列式因子。2、不變因子中所有因子稱為 的不變因子組。經過初等變換不改變多項式矩陣的秩和行列式因子,有相同的行列式因子或不變因子是 與 等價的充要條件...
在他的分類方法中他引進了初等因子和不變因子的概念,但他沒有證明“不變因子組成兩個二次型的不變數的完全集”這一結論。1858年,維爾斯特拉斯對同時化兩個二...
二、不變因子,行列式因子與初等因子8.2 矩陣相似的條件一、矩陣相似與又一矩陣等價之間的關係二、矩陣相似的充要條件8.3 矩陣的Jordan標準形一、Jordan標準形及其...
7.3不變因子7.4矩陣相似的判定7.5初等因子7.6若當(Jordan)標準形7.7最小多項式習題7(A)第8章二次型8.1二次型及其矩陣表示...
7.3不變因子 (242) 7.4矩陣相似的判定 (245) 7.5初等因子 (247) 7.6若當(Jordan)標準形(251) 7.7最小多項式(256) 習題7(A)(259)第8章 二次型(26...
傳遞群是集合Ω在置換群G下保持不變的某些子集。 弗羅貝尼烏斯群(Frobenius ...因此,半正則群G的階是|Ω|的因子。若G是Ω上的正則群,則|Ω|=|G|。...
三、不變因子57四、初等因子59§2.6Jordan標準形的理論推導60一、矩陣的相似性條件60二、Jordan標準形64三、最小多項式68習題二70...
§ 3 λˉ矩陣的不變因子§ 4 矩陣的若當標準型二、 典型範例與習題選解 [2] 參考資料 1. 微積分 .噹噹網[引用日期2019-07-26] 2. 簡介 .復旦大學...
2.3.3 不變因子和初等因子2.3.4 Jordan 標準形2.4 解題方法指導2.5 內容結構框圖2.6 典型題剖析2.7 答疑解惑2.8 《教材》習題全解...
