多項式矩陣即元為多項式的矩陣。
基本介紹
- 中文名:多項式矩陣
- 外文名:Polynomial matrix
- 類型:計算機科學
- 學科:跨學科
- 性質:矩陣
- 概念:元為多項式的矩陣
介紹








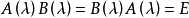



多項式矩陣
運算註解
初等變換
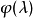
多項式矩陣的秩


多項式矩陣的逆矩陣

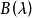







多項式矩陣的等價



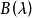

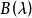


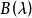
多項式矩陣的行列式因子







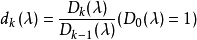



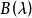




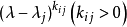
多項式矩陣的標準型



多項式矩陣即元為多項式的矩陣。








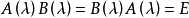



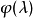



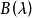










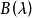

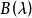


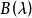







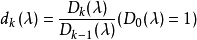



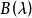




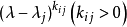



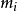
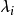
多項式矩陣即元為多項式的矩陣。...... 的多項式。多項式矩陣,也稱為λ-矩陣、矩陣係數多項式(不是矩陣多項式),是數學中矩陣論里的概念,指係數是多項式的方塊矩陣。...
矩陣多項式(matrical polynomial)是一種特殊矩陣。設A0,A1,…,As是數域P上的m×n矩陣,λ是一個文字,則A0λs+A1λs-1+…+As-1λ+As稱為矩陣多項式。矩陣...
矩陣多項式函式(matrix polynomial function)是一種基本而重要的矩陣函式。...... 矩陣多項式函式(matrix polynomial function)是一種基本而重要的矩陣函式。...
傳遞函式矩陣(transfer function matrix)表示線性定常控制系統輸入向量對狀態向量、輸入向量對輸出向量傳遞關係的矩陣。用於多輸入多輸出控制系統的分析研究。...
在數學中,由若干個單項式相加組成的代數式叫做多項式(若有減法:減一個數等於加上它的相反數)。多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就...
澤爾尼克多項式是一個以1953年獲諾貝爾物理學獎荷蘭物理學家弗里茨·澤爾尼克命名的正交多項式,分為奇、偶兩類。...
矩陣函式的概念與通常的函式概念類似,不同在於矩陣函式的自變數和因變數都是n階矩陣。矩陣函式一般用冪級數表示。矩陣函式與矩陣值函式是矩陣理論的重要內容,它們在...
西爾維斯特矩陣,是與兩個多項式相關的矩陣,從這個矩陣可以知道這兩個多項式的一些信息。...
λ矩陣以-matrix)亦稱多項式矩陣.以多項式為元素的矩陣。...... λ矩陣以-matrix)亦稱多項式矩陣.以多項式為元素的矩陣。階又矩陣A(.l),若存在P上的n階穴矩陣Q...
多項式算法(polynomial algorithm)亦稱有效算法或好算法,是一類計算時間不超過始數據量的一個多項式的算法,算法滿足以下的條件:存在多項式P,使算法的時間複雜性函式f(...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
並矢矩陣(dyadic matrix)非奇異多項式矩陣的一種特殊表示形式.當 其中A。和A,為實常數矩陣,A。非奇異,則GCs)為並矢矩陣.如果被控制對象的傳遞函式矩陣是並矢...
多項式插值法是一種搜尋方法。指用插值多項式φ(t)的極小點逼近尋求函式f(t)的極小點的方法具體做法是:求φ′(t)=0的根,作為f(t)的極小點的近似,重複...
方塊矩陣,或簡稱方陣,是行數及列數皆相同的矩陣。由n*n矩陣組成的集合,連同矩陣加法和矩陣乘法,構成環。 除了 n = 1,此環並不是交換環。...
赫爾維茨矩陣是由Adolf Hurwitz在1895年建立的,其矩陣元素是來源於實數多項式的係數。...
線性變換多項式是一種特殊的線性變換。線性變換是線性代數研究的一個對象,即向量空間到自身的保運算的映射,線性變換的冪滿足指數法則。...
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。...
證明:利用范德蒙德矩陣和代數學基本定理即得。當 的值來自某個函式 ,且f(x)具有n+1階連續導數時,下面的定理可以用來計算多項式插值的(截斷)誤差。...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
車多項式(rook polynomials)是美國數學家John Riordan在研究西洋棋中車的禁位排列問題時創立的多項式。設B為n個對象受限制的排列問題的棋盤,rk(B)(k=1,2,…,...
多項式最小二乘法(method of least square byusing polynomials)最小二乘法的一種.指擬合曲線為多項式的最小二乘方法...
矩陣變換是線性代數中矩陣的一種運算形式。線上性代數中,矩陣的初等變換是指以下三種變換類型 :(1) 交換矩陣的兩行(對調i,j,兩行記為ri,rj);(2) 以一個非...
域多項式(field polynomial)一種特殊多項式.指在域擴張下,由一個元素所決定的多項式一個有限域擴張K/F,K可以看成F上的有限維向量空間.設w是它的一個基,對於x...
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數,通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A的...
