基本介紹
- 中文名:線性變換多項式
- 外文名:polynomial of a linear transformation
- 適用範圍:數理科學
簡介
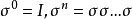
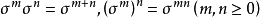
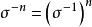
示例
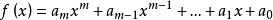
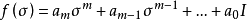
關係
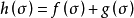
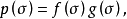
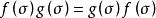
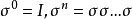
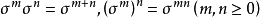
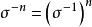
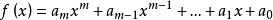
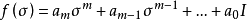
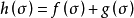
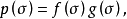
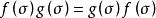
線性變換多項式是一種特殊的線性變換。線性變換是線性代數研究的一個對象,即向量空間到自身的保運算的映射,線性變換的冪滿足指數法則。...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
線性變換行列式是一種特殊行列式,指線性變換矩陣的行列式。設σ是數域P上的n維線性空間V的線性變換,因為相似矩陣有相等的行列式,所以可以把σ關於V的任意基的矩陣的...
1. 黃堃,楊錦偉.線性變換在互素多項式下核的直和分解及套用[J].平頂山學院學報,2008(05):42-44. 2. 劉瓊,呂登峰.互素多項式在線性變換下的維數特徵[J]....
多項式代數,是高等代數的一個分支。在高等代數中,一次方程組(也稱為“線性方程組”)被發展成為線性代數理論;而二次以上的一元方程(也稱為“多項式方程”)被發展...
可分解線性變換(decomposable linear trans-formation)一種特殊的線性變換.即可用來對線性空間做直和分解的線性變換.設V是域P上的n維線性空間,a是V的線性變換,V;}...
不可約線性變換(irreducible linear transfor-mation)亦稱不可分解線性變換一種特殊的線性變換.設V是域P上的n維線性空間,aEHom,}<V,V),若除。,V外,不存在a...
F的一個線性變換.係數矩陣A= (ar;)的特徵多項式稱為二的域多項式.二的域多項式與二所在的域有關,而與基的選取無關.若f(x)是二EK的域多項式,m(二)是二...
單模變換是保持體積的向量空間的線性變換,取決於任意單位模矩陣的基的變換。對m×n多項式矩陣Q(s),引入m×m單模陣R(s)和n×n單模陣T(s),則稱R(s)Q(s)...
介紹 半單變換(semi-simple transformation)一類特殊的線性變換.設V是域P上的n維線性空間,。E HomP<V,V),若。恰有n個線性無關的特徵向量,則稱。為半單變換...
對合變換(involutory transformation)是一種特殊的冪麼變換。冪麼變換是一種特殊的可逆線性變換。可逆線性變換亦稱非退化線性變換,或滿秩線性變換。一種特殊的線性...
本書是作者在中國科學技術大學數學系多年教學的基礎上編寫成的.它由多項式、行列式、矩陣、線性空間、線性變換、Jordan標準形、Euclid空間、酉空間和雙線性函式等九章...
《線性代數與幾何(下)》分上、下兩冊出版,對應於兩個學期的教學內容。下冊在上冊的基礎上更深入地介紹線性空間和線性變換的理論,具體包括一元多項式,相似標準形,...
變換矩陣是數學線性代數中的一個概念。線上性代數中,線性變換能夠用矩陣表示。如果T是一個把Rn映射到Rm的線性變換,且x是一個具有n個元素的列向量 ,那么我們把m...
特別地,複數域上的線性空間中,如果其線性變換 的特徵多項式沒有重根,則 在某組基下矩陣為對角陣。3)如果 是 的不同特徵值,而 是線性變換 屬於特徵值 的線性...
第3章 多項式和有理函式3.1 單變數多項式3.2 帶餘除法3.3 多變數多項式3.4 因式分解3.5 多項式函式第4章 向量空間4.1 向量空間和線性變換4.2 商空間...
哈密頓(W.R.Hamilton)在他所著《四元數講義》一書中,涉及線性變換滿足它的特徵多項式的問題,凱萊(A.Cayley)在1858年的一篇文章中,對n=3的情形驗證了此定理,...
第七章 線性變換 1. 線性變換的定義與性質 2. 線性變換的矩陣 3. 特徵值與特徵向量 4. 對角矩陣 5. 線性變換的值域、核與不變子空間 6. 最小多項式 7....
注重理論聯繫實際,重視在實踐教學中培養學生的實踐能力和創新能力.全書共分9章,其內容包括行列式、矩陣、線性空間、線性變換、多項式、特徵值、λ 矩陣、二次型和...
內容共分九章,包括多項式、行列式,線性方程組、矩陣、二次型、線性空間、線性變換、人一矩陣、歐幾里得空間等知識.內容編排上與北京大學數學系幾何與代數教研室編寫的...
