單模變換是保持體積的向量空間的線性變換，取決於任意單位模矩陣的基的變換。對m×n多項式矩陣Q(s)，引入m×m單模陣R(s)和n×n單模陣T(s)，則稱R(s)Q(s)，Q(s)T(s)和R(s)Q(s)T(s)為Q(s)的單模變換。單模變換線上性時不變系統復頻率域理論中具有重要作用。
基本介紹
- 中文名：單模變換
- 外文名：unimodular transformation
- 所屬學科：數學
- 相關概念：初等變換，單模矩陣等
定義,相關結論,
定義
定義1[單模矩陣] 方多項式矩陣Q(s)為單模陣若且唯若detQ(s)=c即為獨立於s的非零常數。單模陣Q(s)的逆
Q-1(s)為多項式矩陣，且Q-1(s)也為單模陣。同維單模陣的乘積陣為單模陣。
定義2[單模變換] 對m×n的多項式矩陣Q(s)，設m×m的多項式矩陣R(s)和n×n的多項式矩陣T(s)為任意單模陣，則稱R(s)Q(s)，Q(s)T(s)，和R(s)Q(s)T(s)為Q(s)的單模變換。
注: 在基於多項式矩陣方法的線性系統復頻率域理論中，單模變換是用來簡化和推證的一個基本手段。
相關結論
進而，基於初等變換屬性給出如下一些有用推論，它們為單模陣和多項式矩陣單模變換提供了直觀解釋。
推論1[初等變換屬性] 初等矩陣的乘積陣為單模陣，對矩陣Q(s)作一系列行初等變換等價於Q(s)左乘相應單模陣即相應左單模變換，對矩陣Q(s)作一系列列初等變換等價於Q(s)右乘相應單模陣即相應右單模變換。
推論2[單模變換屬性] 對矩陣Q(s)左乘單模陣即左單模變換，可等價地化為對Q(s)的相應一系列行初等變換。對矩陣Q(s)右乘單模陣即右單模變換，可等價地化為對Q(s)的相應一系列列初等變換。
推論3[單模變換和初等變換關係] 矩陣Q(s)的單模變換和初等變換存在如下對應關係：
R(s)Q(s)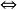
對Q(s)作等價一系列行初等變換；
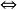
Q(s)T(s)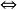 對Q(s)作等價一系列列初等變換；
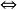
R(s)Q(s)T(s) 對Q(s)同時作等價一系列行和列初等變換。
初等變換
m×n多項式矩陣Q(s)的初等變換有三種類型。
①交換Q(s)的兩行或兩列。生成m×m行初等矩陣E1r和n×n列初等矩陣E1c：
E1r=對應“Q(s)交換行i和行j”為“交換Im列i和列j導出的常陣”
E1c=對應“Q(s)交換列i和列j”為“交換In行i和行j導出的常陣”
則
Q(s)在行i和行j交換後得到矩陣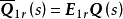
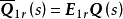
Q(s)在列i和列j交換後得到矩陣
②用非零常數c∈R乘於Q(s)某行或某列。生成mxm行初等矩陣E2r和n×n列初等矩陣E2c：
E2r=對應“c乘於Q(s)行i”為“c乘於Im列i導出的矩陣”
E2c=對應“c乘於Q(s)列j”為“c乘於In行j導出的矩陣”
則
Q(s)在c乘於行i後得到矩陣
Q(s)在c乘於列j後得到矩陣
③用非零多項式d(s)∈R(s)乘於Q(s)的某行/某列所得結果加於另某行/另某列。生
成mxm行初等矩陣E3r和n×n列初等矩陣E3c：
E3r=對應“d(s)乘以Q(s)行i加於行j”為“d（s）置於Im列i和行j交點導出矩陣”
E3c=對應“d(s)乘以Q(s)列i加於列j”為“d(s)置於In行i和列j交點導出矩陣”
則 ，
Q(s)在“d(s)乘以Q(s)行i加於行j”後得到矩陣
Q(s)在“d(s)乘以Q(s)列i加於列j”後得到矩陣
。
