對合變換

對合變換(involutory transformation)是一種特殊的冪麼變換。冪麼變換是一種特殊的可逆線性變換。可逆線性變換亦稱非退化線性變換，或滿秩線性變換。一種特殊的線性變換。設V是數域P上的線性空間，σ是V的線性變換。若存在V的變換τ，使στ=τσ=I，其中I為單位變換，則σ稱為可逆線性變換，τ稱為σ的逆變換。

基本介紹

• 中文名：對合變換
• 外文名：involutory transformation
• 領域：數學
• 學科：線性代數
• 性質：特殊的冪麼變換
• 空間：特徵子空間

概念

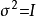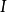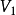對合變換(involutory transformation)一種特殊的冪麼變換。數域P上的n維向量空間V的一個線性變換稱為對和變換，如果，為單位變換。對合變換的特徵值只能是1或-1，且⨁，其中是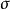的屬於特徵值1的特徵子空間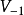，是的屬於特徵值-1的特徵子空間。

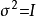
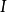
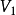
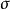
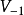
冪麼變換

冪麼變換是一種特殊的可逆線性變換。設V是數域P上的線性空間，σ是V的線性變換。若存在自然數m，使σ^m=I，σ^m-1≠I，I為單位變換，則σ稱為冪麼變換，m稱為冪麼指數。一個線性變換是冪麼變換，若且唯若它的特徵多項式的根是m個m次單位根。

線性變換

線性代數的重要概念之一。設σ是數域P上的線性空間V的一個變換。若對於V中的任意向量α，β與P中的任意數k，有σ(α+β)=σ(α)+σ(β)，σ(kα)=kσ(α)，則稱σ是V的一個線性變換。設σ是線性空間V的一個變換，若對於V中任意向量α，有σ(α)=α，則σ是V的線性變換，稱為恆等變換，亦稱單位變換，記為I。若V的變換σ對於V中的任意向量α，有σ(α)=0，則σ是V的線性變換，稱為零變換，記為0.線性變換是歐氏幾何中的變換、解析幾何中的某些坐標變換、數學分析中的某些變數代換以及其他數學分支中某些類似的變換的抽象、概括與推廣。數域上線性空間的線性變換可以推廣為同一個域上的兩個不同線性空間的線性映射。線性變換不僅是線性代數的主要研究對象之一，也是數學中的一個重要的概念。近代數學中的許多分支的研究對象，如泛函分析中的線性運算元。同調代數中的模同態等都與線性變換有密切的聯繫。

可逆線性變換

可逆線性變換亦稱非退化線性變換，或滿秩線性變換。一種特殊的線性變換。設V是數域P上的線性空間，σ是V的線性變換。若存在V的變換τ，使στ=τσ=I，其中I為單位變換，則σ稱為可逆線性變換，τ稱為σ的逆變換。V上的可逆線性變換σ的逆變換仍為V的線性變換，且是惟一的，記為σ.線性空間的可逆線性變換的集合，對於變換的乘法構成乘法群，稱為非奇異線性變換群。

線性空間

亦稱向量空間。它是線性代數的中心內容和基本概念之一。設V是一個非空集合，P是一個域。若：

1.在V中定義了一種運算，稱為加法，即對V中任意兩個元素α與β都按某一法則對應於V內惟一確定的一個元素α+β，稱為α與β的和。

2.在P與V的元素間定義了一種運算，稱為純量乘法(亦稱數量乘法)，即對V中任意元素α和P中任意元素k，都按某一法則對應V內惟一確定的一個元素kα，稱為k與α的積。

3.加法與純量乘法滿足以下條件：

1) α+β=β+α，對任意α，β∈V。

2) α+(β+γ)=(α+β)+γ，對任意α，β，γ∈V。

3) 存在一個元素0∈V，對一切α∈V有α+0=α，元素0稱為V的零元。

4) 對任一α∈V，都存在β∈V使α+β=0，β稱為α的負元素，記為-α。

5) 對P中單位元1，有1α=α(α∈V)。

6) 對任意k，l∈P，α∈V有(kl)α=k(lα)。

7) 對任意k，l∈P，α∈V有(k+l)α=kα+lα。

8) 對任意k∈P，α，β∈V有k(α+β)=kα+kβ，

則稱V為域P上的一個線性空間，或向量空間.V中元素稱為向量，V的零元稱為零向量，P稱為線性空間的基域.當P是實數域時，V稱為實線性空間。當P是複數域時，V稱為複線性空間。例如，若V為三維幾何空間中全體向量(有向線段)構成的集合，P為實數域R，則V關於向量加法(即平行四邊形法則)和數與向量的乘法構成實數域R上的線性空間。又如，若V為數域P上全體m×n矩陣組成的集合M_mn(P)，V的加法與純量乘法分別為矩陣的加法和數與矩陣的乘法，則M_mn(P)是數域P上的線性空間。V中向量就是m×n矩陣。再如，域P上所有n元向量(a₁，a₂，…，a_n)構成的集合P對於加法：(a₁，a₂，…，a_n)+(b₁，b₂，…，b_n)=(a₁+b₁，a₂+b₂，…，a_n+b_n)與純量乘法：λ(a₁，a₂，…，a_n)=(λa₁，λa₂，…，λa_n)構成域P上的線性空間，稱為域P上n元向量空間。

特徵值

矩陣特徵值概念的推廣，是由運算元決定的一些複數。設T是線性空間X上的運算元，λ是複數。如果X中有非零向量x，使Tx=λx，則稱λ為T的特徵值(或本徵值)，而x稱為相應於λ的特徵向量(或本徵向量)。當T是線性運算元時，相應於特徵值λ的特徵向量再加上零向量構成線性子空間，記為E_λ，稱E_λ為相應於λ的特徵子空間。E_λ的維數稱為特徵值λ的重複度。對有限維空間，求矩陣的特徵值以及與它相應的線性方程組的求解問題線上性代數中已經完全解決。當空間是無限維時，問題變得複雜得多。

特徵子空間

一類重要的子空間。即對應於線性變換的一特徵值的子空間。設V是域P上的線性空間，σ是V的一個線性變換，σ的對應於特徵值λ₀的全體特徵向量與零向量所成的集合，對於V的加法及數量乘法構成V的子空間，稱為σ的對應於特徵值λ₀的特徵子空間，記為V_λ0。若L_λ0={ξ∈V|對某s>0，(σ-λ₀E)ξ=0，E為恆等變換}，則L_λ0是V的子空間，稱為σ對應於λ₀的廣義特徵子空間(或根子空間)。當V為n維線性空間，且σ的特徵多項式f(λ)的全部不同的根λ₁，λ₂，…，λ_r皆屬於P時，則V是對應於λ_i(i=1，2，…，r)的廣義特徵子空間的直和。