基本介紹
李代數












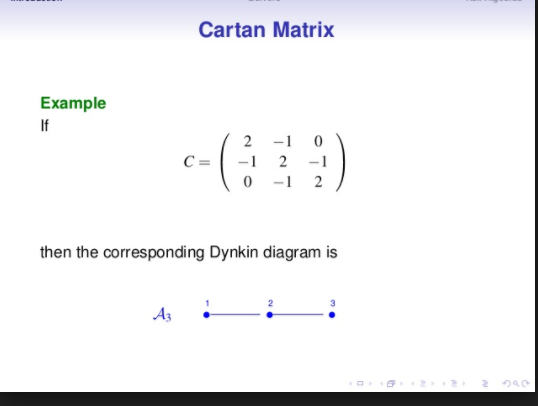












在數學中,嘉當矩陣是由法國數學家埃利·嘉當引入的一類特別矩陣,最大的套用在於李代數的分類理論。在有限維代數的表示理論中,嘉當矩陣另有其它意義。李代數所謂廣義嘉當矩陣是具有下述性質的方陣:各項皆為整數:。對角線上的項等於二...
不可約嘉當矩陣 不可約嘉當矩陣(irreducible Cartan matrix)是1993年公布的數學名詞,出自《數學名詞》第一版。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
若 則A是一個k代數,X是A模.設1,是不可約A模,將L,在叉中作為合成因子的重數動,稱為A的分解數,由全體分解數d;,組成的矩陣(d;;)稱為分解矩陣.若K與k都是A的分裂域且A⑧HK是半單代數,則D'D = C,其中C是A的嘉當矩陣,D'’是D的轉置矩陣.群代數RG的分解矩陣也稱為群G的分解矩陣.
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。嘉當子群(Cartan subgroup)是代數群的一個重要子群。指代數群G的極大環面的連通中心化子。當G是簡約群時,嘉當...
嘉當矩陣(Cartan matrix)是群表示論的一個特殊矩陣,即描述各主不可分解模的不可約成分重數的矩陣。設A是域F上有限維代數,是A的一個主不可分解模,亦即 是正則模A的不可分解直和項,若 是一個不可約A模,則 作為A模 的合成因子的重數 稱為代數A的一個嘉當不變數,由全體嘉當不變數 組成的矩陣 稱為A...
Kac–Moody代數是一個李代數,通常無限維,其定義自(Victor Kac所謂的)廣義根系。Kac–Moody 代數的套用遍及數學和理論物理學。定義 假定以下材料:——一個r秩廣義嘉當矩陣(generalised Cartan matrix) ——— 一個 2n−r 維復向量空間 ——— 的對偶空間 ———中n枚相互線性獨立的元,稱為對偶根(co-root)...
中包含一個 A 的左理想,它在 中的商模給出表示 ;(3)設對 在 內有重數 。我們把這個事實寫作 因為沒有完全可約性,此處我們不使用等號。上式僅表示,作為不可約成分, 在 內的重數為 。顯然 是非負整數。稱為嘉當不變數 (Cartan invariant) 。由 組成的 矩陣 稱為嘉當矩陣 (Cartan matrix)。
外爾一卡茨特徵標公式(Weyl- Kac characterformula)有限維情形外爾特徵標公式的推廣,是表示論的基本公式.若A是可對稱化的廣義嘉當矩陣,L(n)是g(A)的具有最高權n(nEP+的不可約最高權模,則有外爾一卡茨特徵標公式 它的一個特例是 I1n一e(一Q,1 } mult“一藝e(w)e(w(p))一P>,稱為分母恆等式....
若 T 為表示 ,而 在相應的 中出現的重樹為 ,則寫成 稱為分解數,矩陣 稱為分解數矩陣。還可以證明,當 p 模系統(K,P,k)滿足一定條件時,對每個主不可分解表示 ,通過把矩陣 中元素換成其在同態 下的像正好得到 。而且此時還有 由此我們得到嘉當矩陣與分解數矩陣的關係式:。C 是對稱陣。
環(Ring)是一類包含兩種運算(加法和乘法)的代數系統,是現代代數學十分重要的一類研究對象。其發展可追溯到19世紀關於實數域的擴張及其分類的研究。弗羅貝尼烏斯、戴德金、嘉當、哈密頓和T.莫利恩等人是發展超復系理論的主要數學家。簡介 在非空集合R中,若定義了兩種代數運算+和 (不一定為加與乘),且滿足:1、...
附錄25 用嘉當矩陣計算單純李代數的全部正根 附錄26 SU(N)群自身表示生成元的反對易關係 附錄27 實贗正交矩陣的行列式 附錄28 辛群獨立實參數的數目 附錄29 單純李代數的重要性質 附錄30 克萊布施一戈登係數的對稱性質 附錄31 SU(3)群兩伴隨表示直乘的克萊布施一戈登係數 附錄32 蓋爾范德基 附錄33 SU(N)...
李代數(Lie algebra)是一類重要的非結合代數。最初是由19世紀挪威數學家索菲斯·李創立李群時引進的一個數學概念,經過一個世紀,特別是19世紀末和20世紀的前葉,由於威廉·基靈、嘉當、外爾等人卓有成效的工作,李代數本身的理論才得到完善,並且有了很大的發展。簡介 一類重要的非結合代數。非結合代數是環論的...
從(n-1)×n矩陣刪去第k行,而且用(-1)k+1pk表示這樣得出的(n-1)階行列式。那么,從上列的約定便導出一個在有向超曲面F的區域上的(n-1)重積分 它表示了這個區域的“(n-1)維表面積”。 從基本函式 L(x,u)作 且令α=det|αik|,嘉當的測度張量可表成 這樣,這種空間微分幾何便有了發展的基礎...
