基本介紹
- 中文名:Kac-Moody代數
- 外文名:Kac - Moody algebra
- 類別:教育
- 所屬:數學
定義
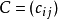
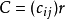
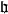
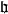
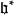
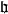
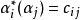
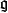
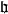
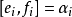
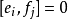
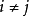
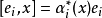
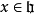
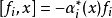
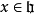
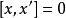
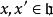
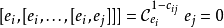
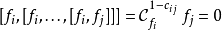
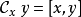
釋義
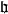
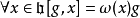
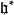
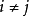
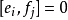

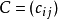
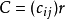
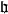
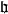
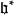
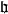
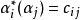
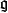
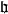
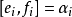
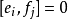
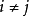
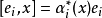
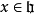
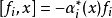
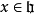
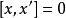
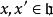
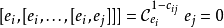
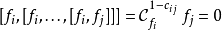
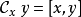
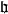
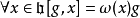
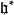
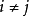
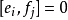
Kac–Moody代數是一個李代數,通常無限維,其定義自(Victor Kac所謂的)廣義根系。Kac–Moody 代數的套用遍及數學和理論物理學。...
無限維李代數內容簡介 編輯 本書是一部權威著作。Kac是該領域的創始人和專家,在無限維李代數和理論物理等領域做出了傑出的貢獻。Kac-Moody代數是近代代數中一個極...
通過推廣Hall與Steinitz的工作,Ringel於1990年引入了finitary代數的Hall代數。後經Ringel,Green,L,usztig等人的發展,Ringel.Hall代數成為量子群和Kac-Moody李代數的一...
全書緊緊以復半單李代數為中心,將其完美的理論和最精彩的內容展現給讀者,同時聯繫於主題,還介紹了它與實半單李代數、代數群、模李代數、Kac-Moody代數、完備李...
頂點運算元代數是1986年RichardBorcherds受二維共形場論中用以插入場之頂點運算元啟發而提出來的代數結構。重要的例子有:晶格頂點運算元代數 仿射Kac-Moody代數的表示的...
晶格頂點運算元代數(用以研究晶格共形場論), 來自仿射Kac-Moody 代數之表示之頂點運算元代數 (用以研究Wess-Zumino-Witten 模型), 來自仿射Virasoro 代數之表示之...
主要內容包括Hall代數的基本理論及其方法,並且著重指出了利用這一理論和方法通過代數表示論去實現Kac-Moody李代數及相應的量子包絡代數;擬遺傳代數及其表示理論,以及這...
維拉宿代數(Virasoro algebra)是單位圓上微分運算元所組成的李代數的中心拓展,在複數域上的無限維李代數。這與仿射Kac-Moody代數關係密切(參看Sugawara構造)。Virasoro ...
a:線性代數 b:群論 c:域論 d:李群 e:李代數 f:Kac-Moody代數 g:環論(包括交換環與交換代數,結合環與結合代數,非結合環與非結合代數等)h:模論 i:格論...
盧才輝,印度尼西亞歸僑,福建永定人,1956年回國,教授,首都師範大學數學系主任。長期從事數學教學和有限維可解李代數,KAC-MOODY代數的研究工作,自1985年以來,已培養...
Kac-Moody代數、頂點運算元表示、頂點代數、高維仿射李代數及相關的無窮維李代數、守衡型非線性發展方程等。主持完成國家自然科學基金3項,主持在研國家自然科學基金...
1989年2月 中國科學院系統科學研究所獲博士學位(方向:Kac-Moody代數,導師:萬哲先院士)1985年7月 廈門大學數學系獲碩士學位(方向:李代數,導師:楊錫安教授)...
1993.12 《Kac-Moody代數導引》 萬哲先著 北京:科學出版社 1989.05 《孫子定理和大衍求一術》 萬哲先著 北京:高等教育出版社 1985.11 《代數與數碼》 萬哲...
第14章為仿射李代數(亦稱Kac-Moody代數),內容基本與第13章平行。第15~17章,討論的主題都是WZW(Wess-Zumino.Witten)模型。WZW模型是二維共形場論中另一個最...
主講過的研究生課程主要有:《模、範疇和同調代數》、《李代數及其表示理論》、《模李代數及其表示》、《Kac-Moody代數》、《李超代數》、《量子群》、《現代數學...
晶格頂點運算元代數(用以研究晶格共形場論), 來自仿射Kac-Moody 代數之表示之頂點運算元代數 (用以研究Wess-Zumino-Witten 模型), 來自仿射Virasoro 代數之表示之...
近世代數、高等代數、高代選講、高等數學、初等數學研究、數學教育學;研究生課程:代數學、同調代數、交換代數、復半單李代數、Kac-Moody代數導引、李超代數、表示...
晶格頂點運算元代數(用以研究晶格共形場論), 來自仿射Kac-Moody 代數之表示之頂點運算元代數 (用以研究Wess-Zumino-Witten 模型), 來自仿射Virasoro 代數之表示之...
《超弦和M理論導論》全面細緻地講解超弦理論和該領域的最新研究進展,內容包括四維超弦,Kac-Moody代數,Teichmuller空間和Calabi-Yau流形,M理論和D膜,對偶和BPS關係,...
擔任研究生的課程教學有:《同調代數基礎:模論、範疇論和同調論》、《復半單李代數及其表示論》、《Kac-Moody李代數及其表示論》、《Hopf代數與量子群》,主持過...
晶格頂點運算元代數(用以研究晶格共形場論), 來自仿射Kac-Moody 代數之表示之頂點運算元代數 (用以研究Wess-Zumino-Witten 模型), 來自仿射Virasoro 代數之表示之...
第14章為仿射李代數(亦稱Kac-Moody代數),內容基本與第13章平行。第15~17章,討論的主題都是WZW(Wess-Zumino.Witten)模型。WZW模型是二維共形場論中另一個最...
● 講授本科生課程:近世代數、線性代數、高等數學。● 講授研究生課程:基本代數、 Lie代數、Hopf代數、Galois理論、量子群、.群與代數表示、Kac-Moody李代數、...
他在1992年證明了這個猜想,證明過程中用到他在1986年發展起來的頂點運算元代數以及廣義的卡茨一穆迪(Kac-Moody)代數。博爾切茲得出一系列新的恆等式,它們還與數學物理...
